dh-Materialien
Einführung in Maple
 

Stichworte
(ausgewählte Rechenanweisungen)

 A   B   C   D   E   F   G   H   I   K   L   M 
 N   O   P   Q   R   S   T   U   V   W   Z 

> restart;
  interface(showassumed = 0):
  interface(displayprecision = -1):

Ableiten (siehe Differenzieren)

Absolutbetrag (siehe Betrag)

Abstand  zwischen zwei zueinander passenden geometrischen Objekten
in: Punkte, Geraden und Ebenen

> with(geom3d):
distance(point(R, 2, 3, 4), point(S, 5, 6, 7));

sw01 

Animation
in: Darstellungen einer Funktionenschar

> with(plots):
animate(t*x^2, x = -3..3,
  t = 0..4,
  view = -5..10,
  color = blue,
  frames = 60,
  font = [COURIER, 12]);

Parabeln

Annahmen
in: Konstanten, Variablen und Variablentypen

> assume(a < 0, b < 0):
is (a*b, positive);
simplify(sqrt(x^2)) assuming (x, real);

true
|x|

Ausgabe mit Formatangaben
in: Das Intervallhalbierungsverfahren

> printf("%s%7.3f\n%s", "xyz ", -34.0587302, "next");

  xyz -34.059
  next

Ausmultiplizieren
 in: Termumformungen

> expand((a+b)^2);

sw02 

nach oben
Berechnen einer reellen Zahl
in: Konstanten, Variablen und Variablentypen

> evalf(sqrt(7));

3.141592654

Betrag
 abs in: Rechnen mit komplexen Zahlen
norm in: Rechnen mit Vektoren

> abs(-5);
> with(LinearAlgebra):
Norm(<-2, 1, 2>, 2);
Norm(<-2, 1, 2>);

5
3
2

Bezeichner (siehe Namen, die in Maple vordefiniert sind)

Binomialkoeffizient
 in: Eigenschaften einer Binomialverteilung

> binomial(12, 4);

495

Bogenmaß umrechnen in das Winkelmaß
in: Trigonometrische Funktionen

> convert(Pi/2, degrees);

sw03 

Bruch umrechnen in eine Gleitkommazahl

> convert(1/3, float);

0.3333333333

nach oben
Catalan’sche Konstante
siehe: Konstanten und Umgebungsvariablen: Catalan

> evalf(Catalan, 50);

sw04 

nach oben
Datentyp überprüfen
in: Konstanten, Variablen und Variablentypen

> whattype(4.78);

float

Determinante einer Matrix
in: Rechnen mit Matrizen

> with(LinearAlgebra):
Determinant(<<2| 1>, <3| 4>>);

5

Differentialgleichung lösen
in: Differentialgleichungen

> dsolve(f(x)^3 - D(f)(x) = 0, f(x));

sw05 

Differenzieren einer Funktion
in: Differenzieren von Funktionen und Funktionstermen

> D(sin);

cos

Differenzieren eines Funktionsterms
in: Differenzieren von Funktionen und Funktionstermen

> diff(sin(x), x);

cos(x)

nach oben
Ebene, definiert durch eine Koordinatengleichung
in: Der Schnitt von Ebenen

> with(geom3d):
plane(E, -1/4*x + 1/5*y + z  = 1, [x,y,z]);
Equation(E);

sw06

Ebene, definiert durch zwei Geraden
in: Der Schnitt von Ebenen

> with(geom3d):
point(P, 0, 0, 1):
line(g1, [P, [0,5,-1]]):
line(g2, [P, [4,0,1]]):
plane(E, [g1, g2]);
Equation(E, [x, y, z]);

sw07 

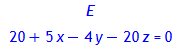
Eliminieren
 in: Geradenscharen

> eliminate({2*x-y = 1, x+y = 2}, {x});

sw08 

Ersetzen
 in: Funktionen und Funktionsterme

> subs(z = 2*a*sqrt(b), z^2 - b = a);

sw09 

nach oben
Fakultät

> factorial(3);
49!;

sw10

Faktorisieren
 in: Termumformungen

> factor(b^2 - a^2);
ifactor(47686234523);

sw11 

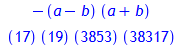
Folge (siehe Zahlenfolge)

Formatierte Ausgabe (siehe Ausgabe mit Formatangaben)

For-To-Do-Schleife
 in: Differenzieren von Funktionen und Funktionstermen

> s:= 0:
for i from 1 to 4 do s:= s + i od:
s;

10

Funktionen

> ?inifcns;

Funktion definieren
in: Funktionen und Funktionsterme

> f:= x -> x^2 + 3;

sw12 

Funktionsterm definieren
in: Funktionen und Funktionsterme

> f(x):= x^2 + 3;

sw13 

nach oben
Genauigkeit (siehe Rechengenauigkeit definieren)

Gerade, definiert durch Stütz- und Richtungsvektor
in: Relative Lage von Geraden

> with(geom3d):
  line(g, [point (A, [-1, 3, 7]), [-3, -5, 2]]);
Equation(g, t);
x:= <op(%)>;

sw14 

Gleichung definieren
in: Rechnen mit Gleichungen

> x:= 'x':
  gl:= x+1 = 3*x;

sw15 

Gleichung mit einer Variablen lösen
in: Rechnen mit Gleichungen

> solve(x^2 + 4*x = 2);
fsolve(x^2 + 4*x = 2);

sw16

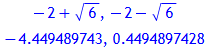
Gleichungssystem (siehe Lineares Gleichungssystem mit zwei Variablen)

Grad eines Polynoms
in: Rechnen mit Polynomen

> degree(x^5 + x);

5

Grenzwert einer Zahlenfolge
in: Eigenschaften der Konstanten infinity

> limit(1/n, n = infinity);

0

Größter gemeinsamer Teiler (GgT)

> igcd(36, 60);

12

nach oben
Horner-Schema
in: Rechnen mit Polynomen

> pol:= 2*x^6 + 5*x^3 - 6*x^2:
convert(pol, horner, x);

sw17 

nach oben
If-Then-Else
in: Die Fibonacci-Zahlen

> k:= 7:
if k = 3 then text:= "k gleich 3"
else text:= "k ungleich 3"
fi:
text;

sw18 

Integrieren
Int in: Unbestimmte Integrale
int in: Berechnung von Flächeninhalten

> Int(1/x, x = 1..2);
int(1/x, x = 1..2);

sw19

Intervalle reeller Zahlen

> x:= ’x’:
assume(x in RealRange(-infinity, Open(0)));
is (x, negative);

true

nach oben
Kettenbruch
in: Lösungen einer Pell’schen Gleichung

> with(NumberTheory):
  cf:= ContinuedFraction(sqrt(19));
  Term(cf, periodic); 

sw21 
sw20

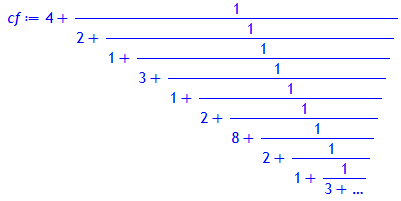
Kleinstes gemeinsames Vielfaches (KgV)

> ilcm(36, 60);

180

Koeffizient eines Polynoms
in: Rechnen mit Polynomen

> coeff(x^3 + 4*x^2 - 5*x, x, 2);

4

Kombinationen
in: Keno

> with(combinat):
randcomb(49, 6);
choose([a, b, c]);

sw22

Kreuzprodukt
 in: Rechnen mit Vektoren

> with(LinearAlgebra):
CrossProduct(<1| 2| 3>, <3| 2| 1>);

sw23

Kugel
 in: Kugeln, Ebenen und Geraden

> with(geom3d):
  x:= 'x':
sphere(K, [point(M, 2, 3, -2), 4]);
Equation(K, [x, y, z]);

sw24 

nach oben
Lagebeziehungen zwischen Geraden und Ebenen
zu überprüfen mit Intersection, AreParallel, ArePerpendicular, AreSkewLines
in: Punkte, Geraden und Ebenen

Lineares Gleichungssystem mit zwei Variablen
 in: Lineares Gleichungssystem mit zwei Variablen

> x:= 'x': y:= 'y':
  gl1:=  2*x - 3*y = 5:
gl2:= -3*x + 5*y = 2:
LGS:= {gl1, gl2};
solve(LGS, {x, y});

sw25

Liste
 in: Mengen, Listen und Folgen

> liste:= [x, y, z];

sw26 

nach oben
Matrizen multiplizieren
in: Rechnen mit Matrizen

> with(LinearAlgebra):
Multiply(<<2|3>, <1|4>>, <2, 1>);

sw27 

Menge
in: Mengen, Listen und Folgen

> menge:= {1, 2, 3, 5, 7};

sw28 

Mengenoperationen
 in: Das Sierpinskidreieck

> {a, b} union {b, c};
{A, B, C, D} minus {B, D};
{1, 2, 3, 4} intersect {2, 4, 6, 8};

sw30 

Mittelpunkt der Strecke zwischen zwei Punkten
 in: Punkte im Raum

>  point(A, 0, 5, -5):
   point(B, 5, 0, -5):
 midpoint(C, A, B):
 coordinates(C);

sw31 

Mittelwert einer Funktion auf einem Intervall

>  with(Student[Calculus1]):
 FunctionAverage(sin(x), x = 0..Pi);

sw32 

nach oben
Namen, die in Maple vordefiniert sind

> ?ininame;

Natürlicher Logarithmus als komplexwertige Funktion
in: Rechnen mit Zahlen

> ln(1);
ln(-1);

sw60

Nenner eines Bruches
in: Rechnen mit Brüchen

> denom(z/n);

n

Norm (siehe Betrag)

Normdarstellung einer Dezimalzahl
in: Rechnen mit Zahlen

> .34E5;

34000.

nach oben
Operanden in Ausdrücken
op in: Rechnen mit Polynomen
nops in: Funktionalisieren von Messdaten

> op(2, {A, B, C});
nops({A, B, C});
op(3, r + s + t + u);
nops(r + s + t + u);

B
3
t
4

nach oben
Permutationen

> with(combinat):
permute([a, b, c], 2);

sw33 

Polynomdivision
 in: Rechnen mit Polynomen

> convert((x^2+3)/(x+5), parfrac, x);

sw34 

Potenz
 in: Rechnen mit Zahlen

> a^n;

sw35 

Primzahlen
 in: Rechnen mit Zahlen

> isprime(1234567);
nextprime(1234567);
ithprime(3);

false
1234577
5

Prozedur
 in: Rechnen mit komplexen Zahlen

> Summe:= proc(zahl1, zahl2)
  zahl1 + zahl2:
end;
Summe(13, 18);

sw36

Prozentoperator

> 17*71;
%*2;

1207
2414

Prüfen von Zahlen auf bestimmte Eigenschaften

> is(1, prime);  # Primzahl?
is(Pi, float); # vom Typ float?
is(0, even);   # gerade Zahl?

false
false
true

Punkt
 in: Punkte im Raum

> with(geom3d):
point(P, [1, 3, -7]);
coordinates(P);

xw37

nach oben
Quadratische Ergänzung

> q:= 3*x^2 + 2*x + 4;  
q:= Student[Precalculus][CompleteSquare](q);


sw38

Quadratwurzel

> sqrt(169);
sqrt(6);

sw39

nach oben
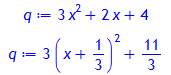
Randbedingungen (siehe Annahmen)

Rechengenauigkeit definieren

> interface(displayprecision = -1):
  Digits:= 20;
0.1234567^2;
sin(0.01);
Digits:= 10;
0.1234567^2;

stichworte55 

Reihe
Sum in: Unbestimmte Integrale
sum in: Berechnung von Flächeninhalten

> Sum(a^2, a = 1..100);
sum(a^2, a = 1..100);

sw41 

nach oben
Schaubild einer Funktion zeichnen
in: Funktionen und Funktionsterme

> plot(sin(x)/x, x = -10*Pi..10*Pi);

sw42 

Schlüsselwörter

> ?keywords;

Schnittpunkt zweier Geraden
in: Relative Lage von Geraden

> with(geom3d):
line(g, [point(P1, 0,1,1), [1,0,1]]):
line(h, [point(P2, 4,2,4), point(Q, 6,3,5)]):
intersection(S, g, h);
coordinates(S);

S
[2, 1, 3]

Skalarprodukt
 in: Rechnen mit Vektoren

> with(LinearAlgebra):
DotProduct(<2, 3, 4>, <-2, 1, 5>);

19

Sortieren
 in: Termumformungen

> sort(a*x + b*x^4 + c*x^2);
sort([Ludwig, Erika, Fridolin, Annika]);
sort([3/4, 1/2, 0.3, 1/3]);

sw43

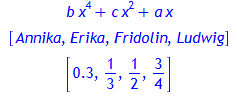
Substituieren (siehe Ersetzen)

Summieren (siehe Reihe)

Systemvariablen (siehe Namen, die in Maple vordefiniert sind)

nach oben
Taylorreihe
 in: Taylorreihen

> taylor(sqrt(x), x = 2, 3);

sw44 

nach oben
Umwandeln eines Bruches in eine Gleitkommazahl und umgekehrt

> convert(1/3, float);
convert(0.25, fraction);

sw45

Umwandeln einer Menge in eine Liste und umgekehrt

> convert({b, a, c}, list);
convert([b, a, c], set);

sw46 

Umwandeln eines trigonometrischen Ausdrucks in einen exponentiellen Ausdruck

> convert(sin(x)*cos(x), exp);

sw47 

Umwandeln einer Zahl in einen Kettenbruch

> convert(5/7, confrac);
convert(Pi, confrac, 20);

sw48 

Umwandeln von Zahlen

> convert(13, binary);
convert(1101, decimal, binary);
convert(A3F, decimal, hex);
convert([15,3,10],base,16,10);

1101
13
2623
[3, 2, 6, 2]

Ungleichung lösen

> solve(18*x^2 > 78*x, x);
solve({18*x^2 > 78*x});

sw50

Unstetigkeitsstellen bestimmen
 in: Untersuchung einer gebrochen-rationalen Funktion

> f:= x -> (x-x^3)/((x-2)*(x+1)):
discont(f(x), x);

{−1, 2}

nach oben
Vektor
 in: Rechnen mit Vektoren

> with(LinearAlgebra):
v:= <2| 3| -1>;  # Datentyp: Vector[row]
v:= <2, 3, -1>;  # Datentyp: Vector[column]

  sw52

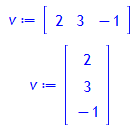
Vektorprodukt (siehe Kreuzprodukt)

Vereinfachen eines Rechenausdrucks
 in: Termumformungen

> simplify(20*a^3/5*a);
  assume(a, real): assume(b, real):
simplify(5*sqrt(a)*sqrt(b)-sqrt(a*b), symbolic);
combine(4*cos(x)^3 - 3*cos(x));

sw53

Verkettungsoperator
in: Differenzieren von Funktionen und Funktionstermen

> f:= x -> x^2 + 3;
(f@g)(x);

sw54 

nach oben
Wahrheitsfunktionen
 in: Wahrheitsfunktionen

> true and false;
true or false;
false implies false;

false
true
true

While-Schleife
 in: Das Heron-Verfahren

> i:= 0;
while (i < 3) do
 i:= i + 1;
od;

sw55

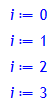
Winkelmaß umrechnen in das Bogenmaß

> convert(45*degrees, radians);

sw56 

 

Winkel zwischen einer Geraden und einer Ebene
in: Punkte, Geraden und Ebenen

> with(geom3d):
line(g, [point(P, 1/3, 6, -2),[0, 1, 2/3]]):
plane(E, -x + 2*y -1/2*z, [x,y,z]):
ww := FindAngle(g, E);
evalf(%);
w:= evalf(convert (%, degrees));

sw57 

Wurzel
in: Rechnen mit Zahlen

> surd(125, 3);

5

nach oben
Zähler eines Bruches
in: Rechnen mit Brüchen

> numer(3/5);

3

Zahlenfolge
 in: Zahlenfolgen

> seq(i^2, i=1..5 );

1, 4, 9, 16, 25

Zufallszahlen
 in: Nichtlineare Regression

> Seed:= randomize();
for i to 10 do rand(6)() od;

sw58

Zusammenfassen (siehe Vereinfachen eines Rechenausdrucks)

Zuweisen

> v:= 23;
assigned(v);
v:= ’v’:
v;
assigned(v);

sw59