Maple-Worksheet: Intervallhalbierung

Einführung in Maple Übungen

Mathematik

Das Intervallhalbierungsverfahren

restart;

Es soll eine Nullstelle der folgenden Funktion bestimmt werden:

>	f:= x -> x^3 + x^2 - 2*x - 1;

>
plot (f(x), x = -3..2.5, labels = ["x", "f(x)"]);

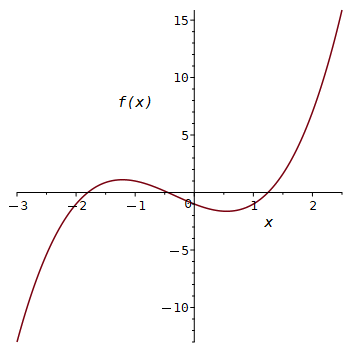
Halbierung des Intervalls [l, r], und zwar so, dass die Vorzeichen von f(l) und f(m) bzw. von f(m) und f(r) verschieden voneinander sind:

>	IH:= proc (l, r) local m; m:= (l + r)/2; if signum(f(l))*signum(f(m)) = -1 then RETURN ([l, m]) else RETURN ([m, r]); fi: end:

Definition des Startintervalls:

>	J[neu]:= [-2.0, -1]: Sukzessive Intervallhalbierung liefert eine Intervallschachtelung: while ((J[neu][2] - J[neu][1]) > 10E-7) do J[alt]:= J[neu]: J[neu]:= IH(J[alt][1], J[alt][2]): printf ("%s%f%s%f%s\n", "[", J[neu][1], ", ", J[neu][2], "]"); od: