dh-Materialien
Maple   Übungen

Lineares Gleichungssystem mit zwei Variablen

> restart;
  interface(displayprecision = 3):

Definition zweier linearer Gleichungen gl1 und gl2 mit den Unbekannten x und y:

> gl1:= 2/5*x = -1/12*y + 3:
gl2:= x -1/2*y = 1/20:
gl1;
gl2;

2/5*x = -1/12*y+3
x-1/2*y = 1/20

Lösen des Gleichungssystems { gl1, gl2 }:

> Gleichungssystem:= {gl1, gl2}:
lgn:= fsolve(Gleichungssystem);

f lhs(lgn[1]) = x then
  xS:= rhs(lgn[1]):
  yS:= rhs(lgn[2]):
else
  xS:= rhs(lgn[2]):
  yS:= rhs(lgn[1]):
fi:
S:= evalf([xS, yS], 4);


S := [5.309, 10.52]

Auflösen der Gleichungen gl1 und gl2 nach y:

> y:= 'y':
y:= solve(gl1, y);
f[1]:= unapply(y, x);

y:= 'y':
y:= solve(gl2, y);
f[2]:= unapply(y, x);

y := -24/5*x+36

linglsys9
linglsys10

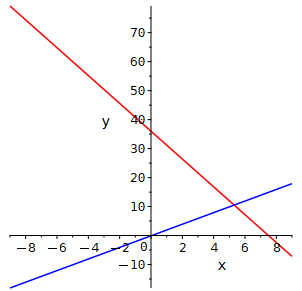
Veranschaulichung von gl1 und gl2 mit Hilfe zweier Geraden;
S ist der Schnittpunkt beider Geraden:

> xr:= round(1.5*xS)+ 1:
  x[links]:= min(-xr, xr):
x[rechts]:= max(-xr, xr):

plot([f[1](x), f[2](x)],
  x = x[links]..x[rechts],
  thickness = 1,
  color = [red, blue],
  axesfont = [Courier, 10],
  labelfont = [Courier, 12],
  size = [300, 300],
  labels = ["x", "y"]);

y:= 'y':
gl1;
gl2;

linglsys11 

2/5*x = -1/12*y+3
x-1/2*y = 1/20