dh-Materialien
Maple   Übungen

Rechnen mit komplexen Zahlen

> restart;

Die imaginäre Einheit i als Lösung der Gleichung  x2 = −1:

> eval(sqrt(-1));

I

Definition einer komplexen Zahl z:

> z:= x + y*I;

z := x+y*I

> cc:= proc(z)
  [evalc(Re(z)), evalc(Im(z))]:
end:

cc(3+2*I);
cc(z);
cc(I);

[3, 2]
[x, y]
[0, 1]

Der Betrag einer komplexen Zahl:

> abs(z);
evalc(%);

abs(x+y*I)

(x^2+y^2)^(1/2)

> z[1]:= x[1] + y[1]*I;
z[2]:= x[2] + y[2]*I;

z[1] := x[1]+y[1]*I
z[2] := x[2]+y[2]*I

Multiplikation von z1 und z2:

> prod:= z[1]*z[2];
evalc(%);
realteil:= evalc(Re(prod));
imaginärteil:= evalc(Im(prod));




Division zweier komplexer Zahlen:

> quot:= z[1]/z[2];
evalc(%);

quot := (x[1]+y[1]*I)/(x[2]+y[2]*I)

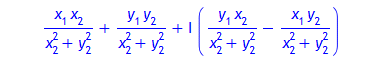
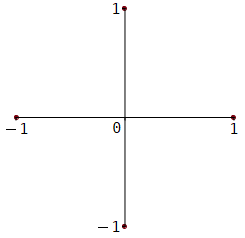
Die Darstellung komplexer Zahlen in der Gauß’schen Ebene:

> plot([cc(1), cc(I), cc(-1), cc(-I)],
  style = point,
  symbol = solidcircle,
  symbolsize = 16,
  scaling = constrained,
  tickmarks = [3, 3],
  size = [250, 250],
  axesfont = [Courier, normal, 12]);

komplzahl19 

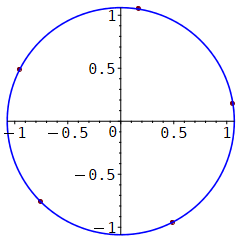
Alle komplexen Zahlen  z  mit der Eigenschaft  |z| = 1:

> z:= x + I*y;
gl:= evalc(abs(z)) = 1: %;
lgn:= solve(gl, y);

f1:= lgn[1]; unapply(f1, x):
f2:= lgn[2]; unapply(f2, x):

plot([f1(x), f2(x)], x = -1..1, y = -1..1,
  labels = ["", ""],
  scaling = constrained,
  color = [red, blue],
  tickmarks = [3, 3],
  size = [250, 250],
  axesfont = [Courier, normal, 12]);

z := x+y*I
(x^2+y^2)^(1/2) = 1
komplzahl23
 f1 := (-x^2+1)^(1/2)
f2 := -(-x^2+1)^(1/2)


 komplzahl26

Komplexe Zahlen in Polardarstellung:

> z;
Phi:= argument(z);
r:= abs(z);
convert(z, polar);
convert(3+2*I, polar);

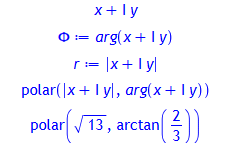
Rechnen mit komplexen Zahlen in Polardarstellung:

> polar(s,phi) + polar(t,psi);
simplify(polar(s,phi)*polar(t,psi));
simplify(polar(s,phi)^3);

komplzahl31 

exp, angewandt auf eine komplexe Zahl  a + bi:

> evalc(exp(a + I*b));

Lösungen der Gleichung z5 = 1 + i:

> z:= 'z':
lgn:= [solve(z^5 = 1+I)]:
for i from 1 to nops(lgn) do
  lgn[i];
od;

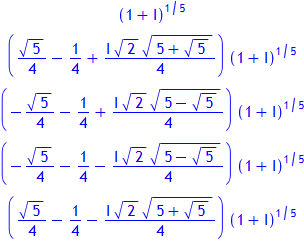
Lösungen von z^5 = 1 + i

Darstellung dieser Lösungen im Argand-Diagramm:

> pkte:= complexplot(lgn,
  font = [Courier, 12]
  style = point,
  symbol = solidcircle,
  symbolsize = 16):
kreis:= plot (abs(lgn[1]),
  coords = polar,
  color = blue):
display (pkte, kreis,
  scaling = constrained,
  size = [250, 250]);

komplzahl33