Änderungsrate

Sieht ein Autofahrer dieses Verkehrsschild, dann heißt es Aufpassen, denn die Straße steigt demnächst steil an. Genauer ausgedrückt: Der Höhenunterschied beträgt 12 Meter bezogen auf 100 Meter in horizontaler Richtung. Dies bedeutet, dass die Straße von der Seite betrachtet so ausschaut:

Anhand dieser Zeichnung erkennt man, dass - mathematisch gesehen - die Darstellung der ansteigenden Straße auf dem Verkehrsschild nicht korrekt ist. Die auf dem Schild dargestellte Steigung beträgt nämlich nicht nur 12/100, sondern ungefähr 4/7, was rund 57% entspricht.

Bezeichnet man den Höhenunterschied mit ∆y und die in horizontaler Richtung zurückgelegte Strecke mit ∆x, dann gilt für die Steigung m:

Das Verhältnis ∆y/∆x gibt an, um wieviele Meter die Höhe bei konstant ansteigender Straße wächst, und zwar relativ zu ∆x. Bei der oben abgebildeten Straße ist m = 6m/50m = 12m/100m = 12/100 = 12%.

Lässt sich die Abhängigkeit irgendeiner Größe y von einer anderen Größe x mithilfe einer Geraden beschreiben (man sagt dann: y hängt linear von x ab), dann gilt

Der Steigungsfaktor m gibt an, wie stark sich y in Abhängigkeit von x ändert:
Im folgenden Beispiel ist m = 4/7 und c = 2.

Diese Definition ist nur dann sinnvoll, wenn sich die Funktionswerte von f innerhalb des Intervalls [a, b] nirgendwo sprunghaft ändern. Mit anderen Worten: die Funktion muss stetig sein.

(f(x₁) − f(x₀))/(x₁ − x₀) ist gleich der Steigung m der Geraden durch die Punkte (x₀|f(x₀) und (x₁|f(x₁). Durch diese Gerade wird eine lineare Funktion g definiert. Falls nun der Abstand zwischen x₀ und x₁ nicht zu groß ist, kann die Funktion f auf dem Intervall [x₀, x₁] durch die lineare Funktion g näherungsweise ersetzt werden. Diese Approximation ist um so besser, je kleiner (x₁ − x₀) gewählt wird.

Aus g(x₀) = mx₀ + c folgt c = g(x₀) − mx₀.
Also gilt g(x) = mx + (g(x₀) − mx₀) = m·(x − x₀) + g(x₀) für x ∈ [x₀, x₁] und damit hat man

Für das zuletzt gezeichnete x-y-Diagramm kann man konkrete Interpretationen (er)finden. Beispielsweise lassen wir zwei Autos auf einer schnurgeraden Straße fahren, die zwei Fahrspuren hat. Beide Autos sollen zur selben Zeit x₀ und an der gleichen Stelle y₀ starten und später (zur Zeit x₁) gleichzeitig an einer bestimmten Stelle y₁ ankommen. Die folgende Zeichnung zeigt beide Autos von oben gesehen zur Startzeit.

Das blaue Auto fährt zunächst langsam los und wird dann immer schneller, das heißt, die Geschwindigkeit des blauen Autos nimmt während der Fahrt zu. Dagegen fährt das schwarze Auto während der gesamten Fahrt gleichförmig, das heißt, die Geschwindigkeit des schwarzen Autos bleibt durchgehend konstant.

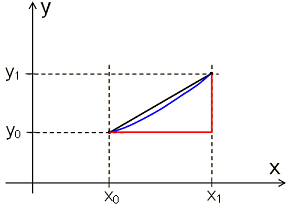
Die Änderungsrate (y₁ − y₀)/(x₁ − x₀) liefert in diesem Beispiel sowohl den konstanten Wert der Geschwindigkeit des schwarzen Autos als auch den Wert der Durchschnittsgeschwindigkeit des blauen Autos auf der Fahrt von y₀ nach y₁. Diese Aussage bleibt auch dann richtig, wenn sich die Geschwindigkeit des blauen Autos zwischendurch sehr stark ändert. Wesentlich ist einzig und allein, dass beide Autos zusammen losfahren und zusammen ankommen.

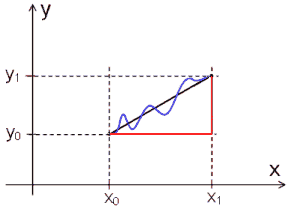
Mit Hilfe der oben definierten Änderungsrate (y₁ − y₀)/(x₁ − x₀) kann man also in Bezug auf ein ausgewähltes Intervall [x₀, x₁] die durchschnittliche Änderung der Funktionswerte einer gegebenen Funktion bestimmen.

Sei irgendeine reellwertige Funktion f auf einem Intervall [a, b] ⊂ ℝ gegeben. Kann man das lokale Änderungsverhalten von f an beliebig gewählten Stellen x₀ ∈ [a, b] berechnen? Mit anderen Worten: Gibt es eine Methode, momentane Änderungsraten von f an denjenigen Stellen zu bestimmen, wo f definiert ist?

Möglicherweise ist es besser verständlich, wenn diese Fragestellung physikalisch formuliert wird, so wie es Sir Isaac Newton (1643 - 1727) getan hat: Gegeben sei ein Körper, der sich nicht gleichförmig bewegt. Gibt es dann eine Methode, die momentane Geschwindigkeit des Körpers zu einem bestimmten Zeitpunkt t₀ zu bestimmen?

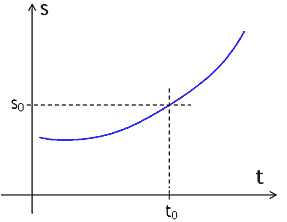
Experimentell betrachtet ist die Sache leicht: Man nehme einen Zeitpunkt kurz vor t₀ und einen Zeitpunkt kurz nach t₀, messe die im Zeitintervall ∆t vom bewegten Körper zurückgelegte Strecke ∆s und hat dann mit

die gesuchte Geschwindigkeit zur Zeit t₀, und zwar um so genauer, je kleiner ∆t gewählt wird. Dieses Messverfahren ist aber in seiner Genauigkeit begrenzt, denn man kann in der Praxis das Zeitintervall ∆t nicht beliebig klein wählen.

Kann der Prozess des Immer-kleiner-Werdens von ∆t bzw. von ∆s theoretisch weiter geführt werden mit dem Ziel, Momentangeschwindigkeiten nicht nur (mit einer unter Umständen kleinen, aber immer bestehenden Messungenauigkeit) zu messen, sondern (exakt) zu berechnen?

Für Gottfried Wilhelm Leibniz (1646 - 1716) war die Frage nach der Berechnung einer Momentangeschwindigkeit gleichbedeutend mit dem Problem, die Steigung der Tangente an einer t-s-Kurve im Punkt (t₀|s₀) zu bestimmen. Die nachfolgende Bildsequenz (die nur bei aktiviertem JavaScript funktioniert) zeigt auf anschauliche Weise, warum das Newton'sche Geschwindigkeitsproblem und das Leibniz'sche Tangentenproblem gleichwertig sind. Im hier dargestellten Beispiel gilt t₀= 1 und s₀ = 1 (Einheiten müssen uns an dieser Stelle nicht interessieren).

Die Idee, das lokale Änderungsverhalten einer Funktion mit Hilfe eines solchen "Funktionenmikroskops" zu untersuchen, stammt von Arnold Kirsch (→ Einführung in Maple, Übung Funktionenmikroskop). Die sukzessive Vergrößerung des abgebildeten Funktionsgraphen um den Punkt (1|1) herum liefert bei genügend starker Vergrößerung fast die Tangente am Funktionsgraphen im Punkt (1|1)! Das Problem, die momentane Änderungsrate der hier gegebenen Funktion an der Stelle 1 zu bestimmen, läuft also anscheinend darauf hinaus, die Steigung der Tangente an dieser Stelle zu berechnen.

Doch der bloße Augenschein allein kann trügen! Dies zeigt das folgende Beispiel aufeinander folgender Treppenkurven, die allesamt die Länge 2 besitzen. Die Folge dieser Treppenkurve nähert sich augenscheinlich beliebig dicht der Quadratdiagonalen, deren Länge der Quadratwurzel aus 2 entspricht. Es gilt aber

Sei eine Funktion f auf einem Intervall [a, b] ⊂ ℝ definiert und a < x₀< b. Wenn die Tangente an der durch y = f(x) definierten Kurve im Punkt P(x₀|f(x₀) in eindeutiger Weise existiert, dann gilt für die Steigung m dieser Tangente:

Hierbei ist Q(x₁|f(x₁) irgendein von P verschiedener Punkt auf dem Graphen von f. Die hier angegebene Formel besagt, dass die Tangentensteigung m, das heißt die „Steigung des Schaubildes der Funktion f an der Stelle x₀“ um so genauer durch den Differenzenquotienten (f(x₁) − f(x₀))/(x₁ − x₀) bestimmt werden kann, je näher der Punkt Q an P heranrückt. Anders ausgedrückt: Wenn x₁ gegen x₀ strebt, dann strebt der Differenzenquotient gegen die Tangentensteigung m. Für diesen Grenzwert, der Ableitung (oder Differentialquotient) der Funktion f an der Stelle x₀ genannt wird, gibt es unterschiedliche Bezeichnungen. Heute wird meistens die erstmals von Joseph Louis Lagrange (1736 - 1813) vorgeschlagene Bezeichnung f´(x₀) oder die von Augustin Louis Cauchy (1789 - 1857) eingeführte Bezeichnung Df(x₀) verwendet. Leibniz benutzte für den Differentialquotienten die Abkürzung dy/dx (gesprochen: „dy nach dx“), die vor allem in der Physik sehr gebräuchlich ist.

Existiert die Ableitung der Funktion f an jeder Stelle x ∈ [a, b], kann man für alle diese x zusammenfassend schreiben:

Durch die Zuordnung x ↦ f´(x) für alle x ∈ [a, b] wird auf [a, b] die Funktion f´ definiert: die Ableitungsfunktion von f. Das Berechnen der Ableitung einer Funktion f nennt man Differenzieren von f (vgl. Einführung in Maple, Übung Differenzieren von Funktionen und Funktionstermen).

Dies alles ist recht anschaulich und nachvollziehbar, doch das Ganze hat einen ganz beträchtlichen Haken: Die hier benutzten Begriffe „um so genauer“, „strebt gegen“, „Grenzwert“ (und so weiter) sind alles andere als präzise und ohne Weiteres im mathematischen Sinn nicht definiert. Die Schlüsselbegriffe für das mathematische Verständnis der Grundlagen dieser Dinge heißen Betrag und Folge.

Die Menge der reellen Zahlen ist mit der auf dieser Menge definierten Relation „≤“ linear geordnet.
Das heißt, es gilt für alle x, y, z ∈ ℝ:

x ≤ y und y ≤ z ⇒ x ≤ z (Transitivität)
x ≤ y und y ≤ x ⇒ x = y (Identitivität)
x ≤ x (Reflexivität)
x, y ∈ ℝ ⇒ x ≤ y oder y ≤ x

Dadurch dass die reellen Zahlen linear geordnet sind, gilt für ℝ die so genannte Trichotomieeigenschaft, das heißt: für zwei reelle Zahlen x und y gilt genau eine der drei Beziehungen x < y, x = y, x > y.

Beweis:
Sei x, y ∈ ℝ. Dann gilt entweder x ≤ y oder y ≤ x oder beides, also x = y.
Falls x ≤ y und x ǂ y folgt x < y; falls y ≤ x und x ǂ y folgt x > y.
Mit anderen Worten: Eine der drei Beziehungen gilt in jedem Fall.

Es ist noch zu zeigen, dass nur höchstens eine der drei Beziehungen gelten kann.
Mit x < y oder x > y folgt definitionsgemäß x ǂ y, das heißt es gilt nicht x = y.
Wenn also x = y gilt, dann gilt weder x < y noch x > y.

Sei nun x < y, das heißt x ≤ y und x ǂ y.
Angenommen, es gilt gleichzeitig auch y < x.
Aus der strengen Ungleichung y < x folgt die schwächere Aussage y ≤ x.
Aus x < y folgt ebenso x ≤ y.
Wegen der Identitivität in ℝ folgt x = y. Widerspruch!

Aufgrund der Trichotomieeigenschaft der reellen Zahlen ist die folgende Definition sinnvoll:

Eine reelle Zahl x mit x > 0 heißt positiv. Ist x < 0, heißt x negativ.

Einige der für ℝ im Kapitel Zahlenmengen bewiesenen Gesetze und Rechenregeln sollen zur besseren Übersicht hier zusammenfassend hingeschrieben werden:

Eigenschaften der rellen Zahlen

G+ (ℝ,+) ist eine Abel'sche Gruppe.

(I)₊ x + (y + z) = (x + y) + z für alle x, y, z ∈ ℝ. (Assoziativität bezüglich „+“)
(II)₊ Es existiert 0 ∈ ℝ mit 0 + x = x für alle x ∈ ℝ. (Existenz eines neutralen Elementes bezüglich „+“)
(III)₊ Zu jedem x ∈ ℝ gibt es ein x* ∈ ℝ mit x* + x = 0. (x* heißt Inverses zu x bezüglich „+“.)
(IV)₊ x + y = y + x für alle x, y ∈ ℝ. (Kommutativität bezüglich „+“)

G· (ℝ\{0},·) ist eine Abel'sche Gruppe.

(I)_* x·(y·z) = (x·y)·z für alle x, y, z ∈ ℝ. (Assoziativität bezüglich „·“)
(II)_* Es existiert 1 ∈ ℝ mit 1·x = x für alle x ∈ ℝ. (Existenz eines neutralen Elementes bezüglich „+“)
(III)_* Zu jedem x ∈ ℝ \ {0} gibt es ein x* ∈ ℝ mit x*·x = 1. (x* heißt Inverses zu x bezüglich „·“.)
(IV)_* x·y = y·x für alle x, y ∈ ℝ. (Kommutativität bezüglich „·“)

D Es gilt das Distributivgesetz.

x·(y + z) = (x·y) + (x·z) für alle x, y, z ∈ ℝ.

N Es gilt 0·x = 0 für alle x ∈ ℝ.

Die Eigenschaften G+, G·, D und N machen ℝ zu einem Körper.
Das Nullelement 0 und das Einselement 1 sind eindeutig bestimmt.
Das zu jedem x ∈ ℝ existierende x* mit x* + x = 0 ist eindeutig bestimmt und wird mit (−x) bezeichnet
Für einen Ausdruck von der Form x + (−y) verwendet man abkürzend die Schreibweise x − y.
Das zu jedem x ∈ ℝ\{0} existierende x* mit x*·x = 1 ist eindeutig bestimmt und wird mit x^-1 bezeichnet.
Aus x·y = 0 folgt x = 0 oder y = 0 (ℝ ist nullteilerfrei).
Es gilt (−x) =(−1)·x für alle x ∈ ℝ.
Hiermit folgt unter anderem: (−(xy)) = (−x)y, 0 = (−0) und (−1)·(−1) = 1. (→ Beweis)

LO ℝ ist linear geordnet.

(T) x ≤ y und y ≤ z

⇒

x ≤ z für alle x, y, z ∈ ℝ (Transitivität bezüglich „≤“).
(I) x ≤ y und y ≤ x ⇒ x = y für alle x, y ∈ ℝ (Identitivität bezüglich „≤“).
(R) x ≤ x für alle x ∈ ℝ (Reflexivität bezüglich „≤“).
(O) x, y ∈ ℝ ⇒ x ≤ y oder y ≤ x

Für alle x, y ∈ ℝ gilt genau eine der drei Beziehungen: x < y, x = y, x > y (Trichotomieeigenschaft von ℝ).
Es wird definiert: |x| = x für x > 0, |0| = 0, |x| = −x für x < 0 (Definition des Betrages von x).
Es gilt: x < y ⇔ x + z < y + z für alle x, y, z ∈ ℝ (Monotonie der Addition).
Es gilt: x > 0 und y > 0 ⇒ xy > 0 für alle x, y ∈ ℝ.
ℝ ist im Gegensatz zu ℕ, ℤ und ℚ nicht abzählbar. (→ Beweis)

VM ℝ ist ein metrischer Raum.

(M1) |y − x| = 0 ⇔ y = x für alle x, y ∈ ℝ.
(M2) |y − x| = |x − y| für alle x, y ∈ ℝ.
(M3) |y − x| ≤ |y − z| + |z − x| für alle x, y, z ∈ ℝ (Dreiecksungleichung).

|y − x| heißt Abstand zwischen x und y.

Beweis der ersten Aussage:
Sei x < y ≤ z. Dann gilt auch x ≤ y ≤ z.
Hieraus folgt wegen der Transitivität x ≤ z.
Angenommen, x = z. Dann folgt x ≤ y ≤ x und wegen der Identitivität hat man x = y.
Nach Voraussetzung ist x < y und dies bedeutet x ǂ y.
Widerspruch! Es muss also x < z gelten.

Die zweite Aussage folgt auf analoge Art.

Beweis der dritten Aussage:
Es gilt x ≤ y ⇔ x + z ≤ y + z.
Aus x ≤ x* folgt demnach x + y ≤ x* + y.
Aus y ≤ y* folgt y + x* ≤ y* + x*.
In ℝ gilt bezüglich "+" das Kommutativgesetz. Also folgt die Behauptung.

Beweis der vierten Aussage:
Sei x ≤ x* und y < y*. Dann gilt auch x ≤ x* und y ≤ y*.
Es folgt x + y ≤ x* + y*.
Angenommen, x + y = x* + y*. Dann folgt
x* + y* = x + y ≤ x* + y ≤ x* + y*.
Wegen der Identitivität folgt x* + y* = x* + y und damit y = y*.
Nach Voraussetzung ist aber y < y*. Widerspruch!
Es folgt also x + y < x* + y* und damit die Behauptung.

Eine reelle Zahl x ist genau dann positiv, wenn (−x) negativ ist.
Ebenso ist x genau dann negativ, wenn (−x) positiv ist.
Zusammen mit der Definition des Absolutbetrages folgt für alle x ∈ ℝ

Beweis:
zu zeigen: x > 0 ⇒ (−x) < 0.
Für eine positive reelle Zahl x gilt x > 0.
Für das Inverse dieser Zahl gilt in jedem Fall (−x) ≤ (−x).
Wegen (U4) folgt hieraus (−x) + 0 < (−x) + x.
Also gilt (−x) < 0, das heißt: (−x) ist negativ.

zu zeigen: (−x) < 0 ⇒ x > 0.
Sei (−x) eine negative reelle Zahl. Dann gilt (−x) < 0.
Also folgt mit (U4): 0 = x + (−x) < x + 0 ⇒ x > 0.

zu zeigen: |x| ≥ 0.
x = |x| für x ≥ 0. Also gilt in diesem Fall auch |x| ≥ 0.
Wenn x negativ ist, dann ist (−x) und nach Definition dann auch |x| positiv.

Üblicherweise schreibt man für das Negative einer reellen Zahl statt (−x) nur −x.
Sei nun ε eine positive reelle Zahl. Dann gilt für alle x ∈ ℝ

Beweis:
"⇒": Sei |x| ≤ ε. Fall 1: x = |x|. Dann folgt x ≤ ε. Wegen ε > 0 gilt −ε < 0 ≤ |x| und damit −ε ≤ x.
Fall 2: x = −|x|. Dann folgt −x ≤ ε und somit −ε ≤ x. Wegen x = −|x| ist x ≤ 0. Also gilt x ≤ ε.
Insgesamt folgt also in jedem Fall −ε ≤ x ≤ ε.
"⇐": Sei −ε ≤ x ≤ ε. Dann folgt |x| ≤ ε sowohl für x = |x| als auch für x = −|x| unmittelbar.

Beweis der ersten Aussage:
Zunächst sei bemerkt, dass x = −y und y = −x zwei zueinander äquivalente Aussagen sind.

Es gilt x = |x| oder x = −|x|, bzw. y = |y| oder y = −|y|.
Also gilt xy = |x|·|y| oder xy = −|x|·|y|.
Im ersten Fall ist xy ≥ 0 und diesem Fall gilt |xy| = xy.
Im zweiten Fall ist xy ≤ 0 und man hat |xy| = −xy = |x|·|y|.

Beweis der zweiten Aussage:
Für x = 0 oder y = 0 ist die Ungleichung offensichtlich wahr.
Unter der Voraussetzung, dass sowohl x als auch y von 0 verschieden sind, gilt |x| + |y| > 0.
Hieraus folgt −(|x| + |y|) ≤ x + y ≤ |x| + |y| und damit |x + y| ≤ |x| + |y|.

Eine Funktion f: ℕ → ℝ nennt man eine Zahlenfolge. Das n-te Folgenglied einer solchen Zahlenfolge wird mit "x_n", die gesamte Folge mit "(x_n)" oder genauer mit "(x_n)_n=0..∞" bezeichnet.

Beweis:
Angenommen, eine konvergente reelle Zahlenfolge (x_n) hat
zwei voneinander verschiedene Grenzwerte x und y.
Dann gilt |x − y| = |(x − x_n) + (x_n − y)| ≤ |x − x_n| + |x_n − y| → 0 (n → ∞).
Also folgt x = y. Widerspruch zur Annahme!

Das Cauchy'sche Konvergenzkriterium besagt, dass eine reelle Zahlenfolge (x_n) genau dann konvergent ist, wenn sie eine Cauchyfolge ist (→ Beweis). Damit wird die Menge der reellen Zahlen zu einem vollständigen metrischen Raum.

Seien (x_n) und (y_n) zwei konvergente Zahlenfolgen mit x_n → x und y_n → y (n → ∞).
Dann sind auch die Folgen (x_n + y_n) und (x_n·y_n) konvergent und es gilt

Falls x_n ǂ 0 für alle n ∈ ℕ und x ǂ 0, so ist auch die Folge (1/x_n) konvergent und es gilt

Beweis der ersten Aussage:
Seien (x_n) und (y_n) konvergent mit x_n → x und y_n → y (n → ∞).
Dann gibt es zu jedem ε/2 ∈ ℝ ein N_x ∈ ℕ bzw. ein N_y ∈ ℕ, so dass
|x_n − x| < ε/2 für alle n ≥ N_xund |y_n − y| < ε/2 für alle n ≥ N_y.
Also gilt für alle n ≥ max(N_x, N_y)
|(x_n + y_n) − (y + x)| = |(x_n − x) + (y_n − y)| ≤ |x_n − x| + |y_n − y| ≤ ε/2 + ε/2 = ε,
was zu beweisen war.

Beweis der zweiten Aussage:
Seien (x_n) und (y_n) konvergent mit x_n → x und y_n → y (n → ∞).
Für alle n ∈ ℕ gilt x_n·y_n − x·y = x_n·y_n − x·y_n + x·y_n − x·y = (x_n − x)·y_n + x·(y_n − y).
Die Folge (y_n) ist konvergent und damit beschränkt.
Es lässt sich also eine reelle Zahl s finden mit |y_n| < s für alle n ∈ ℕ und |x| < s.
Hieraus folgt unter Benutzung der Dreiecksungleichung für jedes n ∈ ℕ:
|x_n·y_n − x·y| ≤ |x_n − x|·s + |y_n − y|·s.
Nach Voraussetzung gibt es zwei natürliche Zahlen N_x und N_y, so dass Folgendes gilt:
|x_n − x| < ε/2s für alle n ≥ N_x und |y_n − y| < ε/2s für alle n ≥ N_y,
wobei die positive reelle Zahl ε beliebig gewählt werden kann.
Sei N = max(N, N_y), dann folgt
|x_n·y_n − x·y| ≤ s·ε/2s + s·ε/2s = ε für alle n ≥ N.

Beweis der dritten Aussage:
Sei (x_n) konvergent mit x_n → x (n → ∞), wobei x ǂ 0 und x_n ǂ 0 für alle n ∈ ℕ.
Dann gibt es ein N, so dass ||x_n|−|x|| ≤ |x_n − x| < |x|/2 für alle n ≥ N.
Die Ungleichung ||x_n|−|x|| < |x|/2 ist äquivalent zu der Aussage −|x|/2 < |x_n|−|x| < |x|/2.
Insbesondere folgt hieraus, dass |x_n| > |x| −|x|/2,
also hat man |x_n| > |x|/2 für alle n ≥ N. Hiermit ergibt sich
|1/x_n − 1/x| = |x − x_n|/|x_n|·|x| ≤ 2·|x − x_n|/|x|².
Sei nun ε > 0 beliebig gewählt. Dann gibt es ein N*, so dass für alle n ≥ N* gilt:
|x − x_n| < min(|x|/2, |x|²·ε/2). Damit hat man für alle n ≥ N*
|1/x_n − 1/x| < |x|²·ε/|x|² = ε.

Jede beschränkte unendliche reelle Zahlenfolge enthält mindestens eine konvergente Teilfolge.
Dies ist der fundamentale Satz von Bolzano und Weierstrass (→ Beweis). Mit diesem Satz lässt sich nachweisen, dass monoton steigende Folgen, die nach oben beschränkt sind bzw. monoton fallende Folgen, die nach unten beschränkt sind, immer konvergent sind (→ Beweis).

Der Begriff der Konvergenz einer Folge wird möglicherweise etwas anschaulicher mithilfe der Begriffe Umgebung und Häufungswert.

Sei ε eine positive reelle Zahl und x₀ ∈ ℝ. Dann heißt die Menge

U_ε(x₀) = {x ∈ ℝ: |x − x₀| < ε}

ε-Umgebung von x₀.

Eine Menge U ⊂ ℝ heißt Umgebung von x₀ ∈ ℝ, wenn U eine ε-Umgebung von x₀ enthält.
Man schreibt dann: U = U(x₀).

p ∈ ℝ heißt Häufungswert der Menge M ⊂ ℝ, wenn in jeder Umgebung U(p) unendlich viele Elemente von M liegen. p ∈ ℝ heißt Häufungswert der Zahlenfolge (x_n), wenn in jeder Umgebung von p unendlich viele Folgenglieder dieser Folge liegen.

Eine Zahlenfolge (x_n) ist also genau dann konvergent, wenn sie beschränkt ist und genau einen Häufungswert hat. Dieser Häufungswert ist dann notwendigerweise der Grenzwert dieser Folge.

Die Zahlenfolge (x_n) konvergiert genau dann gegen x, wenn in jeder Umgebung von x fast alle Glieder der Folge liegen, das heißt: alle Folgenglieder mit höchstens endlich vielen Ausnahmen.

Beweis:
"⇒": Sei (x_n) eine konvergente Folge mit x_n → x (n → ∞) und U irgendeine Umgebung von x.
U(x) enthält nach Definition eine ε-Umgebung von x.
Für dieses ε gilt |x_n − x)| < ε für alle n ≥ N mit passend gewähltem N ∈ ℕ.
Damit hat man x_n ∈ U(x) für alle n ≥ N, und nur höchstens n Ausnahmen liegen nicht in U(x).

"⇐": x ∈ ℝ habe die Eigenschaft, dass in jeder Umgebung U(x) fast alle Folgenglieder der Folge (x_n) liegen.
Sei nun ε eine beliebige positive reelle Zahl.
Dann gibt es höchstens endlich viele x_n, die außerhalb von U_ε(x) liegen.
Diese Folgenglieder seien mit x_m1, x_m2, ..., x_mt bezeichnet.
Für jedes n ∈ ℕ gilt dann |x_n|≤ max( |x| + ε, |x_m1|, |x_m2|, ..., |x_mt|).
Also ist die Zahlenfolge (x_n) beschränkt.

Nach Voraussetzung ist x ein Häufungswert von (x_n).
Angenommen, es gibt einen zweiten Häufungswert y von (x_n) mit y ǂ x,
dann ist d = |y − x| > 0 und für zwei ε-Umgebungen U_ε(x) und U_ε(y) gilt
U_ε(x) ∩ U_ε(y) = { }, wenn ε < d/2 gewählt wird.
Damit liegen in U_ε(x) nicht mehr fast alle Folgenglieder von (x_n). Widerspruch!

Die Folge (x_n) ist somit beschränkt und hat nur einen einzigen Häufungswert,
also konvergiert (x_n) gegen x.

Aus diesem Konvergenzkriterium folgt insbesondere, dass jede Teilfolge einer gegen x konvergenten Zahlenfolge (x_n) ebenfalls konvergent ist und gegen x strebt.

Sei M ⊂ ℝ und x₀ ein Häufungswert von M, a ∈ ℝ und f eine auf M definierte reellwertige Funktion.
Dann konvergiert f(x) genau dann gegen a für x gegen x₀, wenn für jede Zahlenfolge (x_n), die gegen x₀ konvergiert, die Folge (f(x_n)) gegen a strebt.

Beweis:
"⇒": Es sei f(x) → a (x → x₀) und (x_n) sei irgendeine Zahlenfolge mit x_n → x₀ (n → ∞).
Sei ε > 0 beliebig vorgegeben. Dann existiert wegen der Konvergenz von f(x) ein δ = δ(ε) > 0
mit |f(x) − a| < ε für alle x mit |x − x₀| < δ.
Wegen x_n → x₀ (n → ∞) gibt es eine von δ abhängige natürliche Zahl n₀ mit
|x_n − x₀| < δ für alle n mit n ≥ n₀.
Also gilt |f(x_n) − a| < ε für n ≥ n₀ und damit hat man f(x_n) → a (n → ∞).

"⇐": Es gelte nun f(x_n) → a (n → ∞) für jede Folge (x_n), die gegen x₀ konvergiert.
Angenommen, es gilt nicht f(x) → a (x → x₀).
Dann gibt es ein ε > 0, so dass zu jedem δ > 0 ein x^(δ) ∈ M existiert
mit |x^(δ) − x₀| < δ und |f(x^(δ)) − a| ≥ ε.
Mit δ = 1/n hat man |x^(1/n) − x₀| < 1/n.
Hieraus folgt x^(1/n) → x₀(n → ∞).
Nach Voraussetzung gilt dann auch f(x^(1/n)) → a (n → ∞) .
Die Konvergenz von (f(x^(1/n))) bedeutet nach Definition, dass
|f(x^(1/n)) − a| < ε ab einer bestimmten Indexzahl n.
Dies steht im Widerspruch zur Ungleichung |f(x^(1/n)) − a| ≥ ε für n = 1, 2, 3, ...

Sei M ⊂ ℝ, x₀ ein Häufungswert von M und f eine auf M definierte reellwertige Funktion.
Dann ist f offenbar genau dann stetig in x₀, wenn f(x) → f(x₀) (x → x₀).

Aus dem eben bewiesenen Satz folgt das sogenannte Folgenkriterium:
Eine Funktion f ist in x₀ ∈ M genau dann stetig, wenn für jede Folge von Zahlen aus M, die gegen x₀ konvergiert, auch die Folge (f(x_n)) gegen f(x₀) konvergiert.

Beweis:
Es seien Δ₁ und Δ₂ zwei auf M ⊂ ℝ definierte Funktionen mit den Eigenschaften (D1) und (D2).
Für jedes x ∈ M folgt dann (x − x₀)·(Δ₁(x) − Δ₂(x)) = 0 wegen (D2).
Es gilt also Δ₁(x) = Δ₂(x) für alle x, die verschieden sind von x₀.
M ist zulässig und Δ ist in x₀ stetig, also folgt auch Δ₁(x₀) = Δ₂(x₀).
Damit hat man Δ₁(x) = Δ₂(x) für alle x ∈ M.

Eine Funktion Δ, die nur die Eigenschaft (D2) hat, lässt sich immer finden. Das heißt, dass im Hinblick auf die Differenzierbarkeit einer Funktion f in x₀ die Stetigkeit von Δ in x₀ die wesentliche Forderung ist! So wie die Stetigkeit ist auch die Differenzierbarkeit von f eine lokale Eigenschaft. Stimmen zwei Funktionen f₁ und f₂ in einer Umgebung von x₀ überein, so ist entweder keine der beiden in x₀ differenzierbar oder aber beide sind dort differenzierbar und es gilt f₁´(x₀) = f₂´(x₀).

Falls eine Funktion Δ mit den Eigenschaften (D1) und (D2) existiert, so konvergiert der Differenzenquotient

aufgrund des Folgenkriteriums gegen f´(x₀), wenn x gegen x₀ strebt. Als Formel geschrieben:

Sei M ⊂ ℝ zulässig und f eine auf M definierte Funktion.
Wenn f in x₀ ∈ M differenzierbar ist, dann ist f auch in x₀ stetig.

Beweis:
Sei f in x₀ ∈ M differenzierbar, dann existiert eine in x₀ stetige Funktion mit
f(x) = f(x₀) + (x − x₀)·Δ(x) für x ∈ M.

Die Aussage des Satzes ist bewiesen, wenn sowohl das Produkt als auch die Summe zweier stetiger Funktionen wieder stetig ist. Dies folgt aber unmittelbar aus dem Folgenkriterium zusammen mit den Grenzwertsätzen für Folgen.

Demzufolge kann eine in x₀ nicht stetige Funktion dort auch nicht differenzierbar sein.

Eine differenzierbare Funktion f kann oft (aber nicht immer!) mehrmals differenziert werden. Man schreibt dann

f⁽⁰⁾ = f, f⁽¹⁾ =f´, f⁽²⁾ = f´´, ... , f⁽ⁿ⁾ = f^(n-1)´ für n ≥ 1

Sei M ⊂ ℝ zulässig, x₀ ∈ M, k ∈ ℝ sowie f und g zwei auf M definierte Funktionen.
Beide Funktionen seien in x₀differenzierbar.
Dann sind auch f + g, k·f, f·g in x₀ differenzierbar und es gilt

(f + g)´(x₀) = f´(x₀) + g´(x₀)
(k·f)´(x₀) = k·f´(x₀)
(f·g)´(x₀) = f´(x₀)·g(x₀) + f(x₀)·g´(x₀)

Beweis:
Es gibt eine in x₀ stetige Funktion Δ_f mit f(x) = f(x₀) + (x − x₀)·Δ_f(x) für alle x ∈ M
und eine in x₀ stetige Funktion Δ_g mit g(x) = g(x₀) + (x − x₀)·Δ_g(x) für alle x ∈ M.

Damit hat man (f + g)(x) = f(x) + g(x) = (f + g)(x₀) + (x − x₀)·(Δ_f+ Δ_g)(x);
(Δ_f+ Δ_g) ist auch stetig in x₀, also gilt die erste Ableitungsregel (Summenregel).

Mit Δ_f ist auch k·Δ_fin x₀ stetig und es gilt (k·f)(x) = (k·f)(x₀) + (x − x₀)·(k·Δ_f)(x) für alle x ∈ M,
folglich gilt auch die zweite Ableitungsregel.

(f·g)(x)
= (f(x₀) + (x − x₀)·Δ_f(x))·(g(x₀) + (x − x₀)·Δ_g(x))
= (f·g)(x₀) + (x − x₀)·[f(x₀)·Δ_g(x) + Δ_f(x)·g(x₀) + (x − x₀)·(Δ_f·Δ_g)(x)]
Die durch den Ausdruck in der eckigen Klammer definierte Funktion ist in x₀ stetig
und hat dort den Wert f(x₀)·g´(x₀) + f´(x₀)·g(x₀).
Somit ist auch die Produktregel bewiesen.

Wenn f(x₀) ǂ 0, dann gibt es auf Grund der Stetigkeit von f in x₀ ein ε > 0,
so dass f(x) ǂ 0 für alle x ∈ M ∩ U_ε(x₀). Für diese x existiert 1/f und es gilt
1/f(x) − 1/f(x₀) = (f(x₀) − f(x))/(f(x)·f(x₀)).
Nach Voraussetzung ist f(x) − f(x₀) = (x − x₀)·Δ_f(x). Damit folgt
1/f(x) = 1/f(x₀) + (x − x₀)·Δ_f(x)/(f(x)·f(x₀)).
Die durch den Ausdruck Δ_f(x)/(f(x)·f(x₀)) definierte Funktion ist in x₀ stetig
und hat dort den Wert f´(x₀)/f(x₀)², was zu beweisen war.

Wegen f/g = f · 1/g folgt die Quotientenregel unmittelbar aus dem Vorhergehenden.

Seien f: M → ℝ und g: N → ℝ miteinander verkettete Funktionen mit f(M) ⊂ N.
Wenn dann f in x₀ ∈ M und g in f(x₀) ∈ N differenzierbar sind, dann ist g◦f in x₀ differenzierbar und es gilt die Kettenregel:

Beweis:
Es gibt eine in x₀ stetige Funktion Δ_f mit f(x) = f(x₀) + (x − x₀)·Δ_f(x) für alle x ∈ M
und eine in y₀ = f(x₀) stetige Funktion Δ_g mit g(y) = g(y₀) + (y − y₀)·Δ_g(y) für alle y ∈ N.

Hieraus folgt
g(f(x))
= g(f(x₀)) + (f(x) − f(x₀))·Δ_g(f(x))
= g(f(x₀)) + (x − x₀)·Δ_f(x)·Δ_g(f(x)).

Die auf M durch Δ(x) = Δ_f(x)·Δ_g(f(x)) definierte Funktion Δ ist stetig in x₀.
Es folgt die Behauptung.

Beweis (mit vollständiger Induktion):
Induktionsanfang:
f(x) = a·x¹ = a·x ⇒ f´(x) = a ist offensichtlich richtig.
Induktionsvoraussetzung:
Angenommen, die Aussage (a·x^m)´ = a·m·x^(m−1) für x ∈ ℝ sei bereits für ein m ∈ ℕ bewiesen.
Induktionsschluss:
(a·x^(m+1))´
= (a·x^m·x)´
= ((a·x^m)·x)´
= a·m·x^(m−1)·x + (a·x^m)·1
= a·m·x^m + a·x^m= a·(m+1)·x^m= a·(m+1)·x^(m+1)−1, was zu beweisen war.

Wegen der Summenregel folgt unmittelbar die Ableitung einer ganzrationalen Funktion:

(a_n·xⁿ + a_n-1·x^n-1 + ... + a₁·x + a₀)´ = a_n·n·x^n-1+ a_n-1·(n-1)·x^n-2 + ... + a₁

Die folgende Tabelle gibt einen Überblick über die Ableitungen einiger wichtiger Funktionen.