Vektor
 Um
zu entscheiden, ob man das in festem Karton zusammengeschnürte Geschenk noch
als Päckchen versenden kann, braucht man unter anderem die Angabe des
Gewichts: Ein Päckchen darf höchstens 2 Kilogramm wiegen. Wird diese
umgangssprachlich formulierte Aussage physikalisch korrekt formuliert, dann
wird daraus: Die Masse eines Päckchens beträgt höchstens 2 Kilogramm.
Um
zu entscheiden, ob man das in festem Karton zusammengeschnürte Geschenk noch
als Päckchen versenden kann, braucht man unter anderem die Angabe des
Gewichts: Ein Päckchen darf höchstens 2 Kilogramm wiegen. Wird diese
umgangssprachlich formulierte Aussage physikalisch korrekt formuliert, dann
wird daraus: Die Masse eines Päckchens beträgt höchstens 2 Kilogramm.
Interessiert man sich für den Aggregatzustand von Wasser, so ist die Temperatur des Wassers entscheidend. Bei normalem Druck schmilzt Wasser bei 0 Grad Celsius; bei 100 Grad Celsius siedet es.
Wenn ein Monitor mit einer Leistung von 130 Watt durchschnittlich jeden Tag 3 Stunden lang eingeschaltet ist, dann „verbraucht“ allein dieses Gerät pro Jahr die elektrische Energie von etwa 142 Kilowattstunden. Diese Energie kostet Geld, und zwar etwa 40 Euro, wenn man einen Arbeitspreis von 28 Cent pro Kilowattstunde zugrunde legt.
Alle diese Größen (Masse, Temperatur, Leistung, Energie, Geld, Zeit und etliche andere) haben eine gemeinsame Eigenschaft: Wenn man eine solche Größe misst, dann wird das Messergebnis immer durch eine Zahl ausgedrückt (natürlich in Verbindung mit der Einheit, in der die betreffende Größe gemessen wird). Diese Größen heißen skalare Größen.
Wird mit einer solchen skalaren Größe der Zustand irgendeines Körpers beschrieben, dann ändert sich der Wert dieser Größe nicht, wenn man den Körper dreht.
Es gibt Größen, bei denen es im Allgemeinen nicht ausreichend ist, als
Messergebnis nur eine Zahl anzugeben. Ist man zum Beispiel mit dem Auto
unterwegs, dann ist es im Hinblick auf das Fahrziel nicht nur wichtig zu
wissen, wie schnell, sondern auch in welche Richtung man
fährt.
 Solche
Größen, die charakterisiert sind durch Betrag und Richtung, heißen
gerichtete Größen. Beispiele hierfür sind: Geschwindigkeit,
Beschleunigung, Kraft, Impuls, Strom. Die Gewichtskraft eines 2
Kilogramm schweren Päckchens zum Beispiel beträgt etwa 20 Newton und ist
senkrecht zur Erdoberfläche gerichtet.
Solche
Größen, die charakterisiert sind durch Betrag und Richtung, heißen
gerichtete Größen. Beispiele hierfür sind: Geschwindigkeit,
Beschleunigung, Kraft, Impuls, Strom. Die Gewichtskraft eines 2
Kilogramm schweren Päckchens zum Beispiel beträgt etwa 20 Newton und ist
senkrecht zur Erdoberfläche gerichtet.
Gerichtete Größen stellt man am besten mit Hilfe von Pfeilen dar. Die Pfeillänge gibt - in einem bestimmten, frei gewählten Maßstab - den Betrag der jeweiligen Größe an.
![]() Beispiel 1:
Beispiel 1:
Die in der Abbildung eingezeichneten Orte A und B sollen 50 Meter voneinander entfernt sein. Das Auto ist am Ort A momentan 10 Meter pro Sekunde schnell und wird deswegen B innerhalb von 5 Sekunden erreichen, sofern die Geschwindigkeit des Autos konstant beibehalten wird.
![]() Beispiel 2:
Beispiel 2:
Die Wurfbewegung eines Körpers lässt sich
auffassen als Überlagerung zweier unabhängig voneinander ablaufender
Einzelbewegungen: eine gleichförmige
Bewegung (mit konstanter Geschwindigkeit) in Abwurfrichtung und zweitens
eine gleichmäßig beschleunigte Fallbewegung nach „unten“. Zur ersten
Bewegung gehört eine Geschwindigkeit v0, bei der
sich weder die Richtung noch der Betrag ändert. Zur zweiten Bewegung gehört
die Fallgeschwindigkeit vy, deren Betrag linear mit
der Zeit t wächst. Die
Addition beider Geschwindigkeiten liefert zu jedem Zeitpunkt die
resultierende Geschwindigkeit v des Körpers, die stets
tangential zur Bahnkurve des Körpers gerichtet ist.
Der hier beschriebene Sachverhalt, der durch Experimente bestätigt werden kann, wird durch die folgende Konstruktion veranschaulicht. Dargestellt ist der geworfene Körper samt Geschwindigkeitspfeilen zu vier verschiedenen Zeitpunkten. Zur Zeit t = 0 gilt v = v0. Befindet sich der Körper zur Zeit t = 0, also beim Abwurf, im Ursprung eines Koordinatensystems mit waagerechter x-Achse und vertikaler y-Achse, dann hat man die Position des Körpers zur Zeit t mit
x = v0·t·cos(α) und y = v0·t·sin(α) − k·t2.
k ist eine Konstante und v0 ist der Betrag der Geschwindigkeit v0.

Die Benutzung von Pfeilen ist nicht nur bei der Analyse zusammengesetzter Bewegungen von Körpern hilfreich, sondern in der gesamten Physik grundlegend wichtig.
Unter der Voraussetzung, dass wir im so genannten Anschauungsraum arbeiten, also in einem dreidimensionalen euklidischen Raum, der aus Punkten besteht, die wir in jedem Fall paarweise miteinander durch eine (jeweils eindeutig bestimmte) Strecke verbinden sowie deren Abstände wir mit den Längen dieser Strecken messen können und der die Eigenschaft hat, dass zwei zueinander parallele Geraden stets den gleichen Abstand behalten, egal wie weit wir entlang dieser Geraden laufen mögen, kann man folgende anschauliche Definitionen formulieren:
 Ein Pfeil ist definiert durch seinen Anfangspunkt, seine Richtung
und seine Länge. Eine Pfeilklasse besteht aus
sämtlichen Pfeilen, die erstens dieselbe
Richtung und zweitens dieselbe Länge haben.
Jeder Pfeil einer Pfeilklasse a heißt Repräsentant
von a. Der Betrag einer Pfeilklasse a
ist gleich der Länge eines ihrer Repräsentanten. Der Betrag von a
wird mit |a| oder mit a bezeichnet.
Ein Pfeil ist definiert durch seinen Anfangspunkt, seine Richtung
und seine Länge. Eine Pfeilklasse besteht aus
sämtlichen Pfeilen, die erstens dieselbe
Richtung und zweitens dieselbe Länge haben.
Jeder Pfeil einer Pfeilklasse a heißt Repräsentant
von a. Der Betrag einer Pfeilklasse a
ist gleich der Länge eines ihrer Repräsentanten. Der Betrag von a
wird mit |a| oder mit a bezeichnet.
Sei mit MPf die Menge aller Pfeile bezeichnet und seien p, q ∈∈ MPf, dann hat man mit
p ~ q ⇔def p und q sind richtungs- und längengleich
eine Äquivalenzrelation auf MPf definiert. Die Pfeilklassen sind die Äquivalenzklassen bezüglich „~“.
![]() Will
man eine Pfeilklasse darstellen, so zeichnet man in der
Regel nur einen Repräsentanten dieser Pfeilklasse und schreibt
den Namen dieser Pfeilklasse daneben.
Will
man eine Pfeilklasse darstellen, so zeichnet man in der
Regel nur einen Repräsentanten dieser Pfeilklasse und schreibt
den Namen dieser Pfeilklasse daneben.
Wird eine Pfeilklasse a durch den Pfeil repräsentiert, der den Anfangspunkt P und den Zielpunkt A hat, so soll dieser Sachverhalt kurz wie folgt ausgedrückt werden:
a = PA→
Der Betrag von a ist gleich dem Abstand zwischen P und A, das heißt: |a| = |PA|.
Seien a und b zwei Pfeilklassen. Dann wird die Summe von a und b wie folgt erklärt:

Für a = PA→ und b = PB→ gilt also a + b = PA→ + AB→ = PB→.
Sei x repräsentiert durch einen Pfeil PX→ mit dem Anfangspunkt P und dem Zielpunkt X. Dann heißt die durch XP→ repräsentierte Pfeilklasse die Gegenpfeilklasse von x. Diese soll mit x* bezeichnet werden.
Mit zwei beliebigen Punkten P und A und a = PA→ folgt a + a* = PP→, mit anderen Worten: |a + a*| = 0.
Diejenige Pfeilklasse, die den Betrag 0 besitzt, heißt Nullpfeilklasse und wird mit o bezeichnet.
Für jede Pfeilklasse a gilt somit a + a* = o. Ferner gilt a + o = a für alle a.
Sei nun a irgendeine Pfeilklasse und r eine beliebige positive reelle Zahl. Dann soll ra diejenige Pfeilklasse sein, die durch einen Pfeil repräsentiert wird, der r-mal so lang ist wie ein Repräsentant von a und in die gleiche Richtung zeigt. ra kann interpretiert werden als Produkt der Zahl r und der Pfeilklasse a. Diese so genannte skalare Multiplikation (oder S-Multiplikation) einer Pfeilklasse a mit einer Zahl r funktioniert mit folgenden Definitionen sogar für alle reellen Zahlen:
ra =def ra
(−r)a =def ra*
1a =def a
0a =def o
Verabredet man die folgende abkürzende Schreibweise
a − b =def a + (−1)b
dann gilt für alle Pfeilklassen a und b: a − b = a + (−1)b = a + 1b* = a + b*
und es gilt insbesondere a − a = o.
Seien a und b irgendwelche
Pfeilklassen und s und t beliebige reelle Zahlen.
Dann ist sa + tb eine
Linearkombination von a und b.
Für alle Pfeilklassen a, b und c gelten bezüglich der Addition das Kommutativgesetz
a + b = b + a,
und das Assoziativgesetz
a + (b + c) = (a + b) + c.
Beweis:
Seien
P, A und B beliebige Punkte.
a = PA→
und b = AB→.
Wähle Punkt P' so, dass P’B→ = a und PP’→ = b.
Anschaulich bedeutet dies, dass PP’BA ein Parallelogramm darstellt.

Dann gilt a + b = PA→ + AB→ = PB→ = PP’→ + P’B→ = b + a.
Die Idee zum Beweis der Assoziativität ist ganz ähnlich:
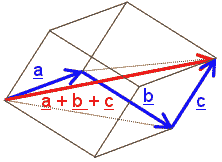
Alle bisherigen Überlegungen und Definitionen waren völlig unabhängig davon, ob unsere Pfeilklassen in einer (nicht gekrümmten) Ebene repräsentiert werden oder in einem (nicht gekrümmten) Raum. Dies ist auch beim Beweis des Assoziativgesetzes so; aber es ist vielleicht anschaulicher, sich unter der hier abgebildeten Figur ein Parallelepiped vorzustellen, also eine räumliche Figur mit acht Eckpunkten und zwölf Kanten, von denen jeweils vier gleich lang und zueinander parallel sind.
Für alle Pfeilklassen a und b und alle reellen Zahlen s und t gelten die folgenden Gesetze:
s(ta) = (s·t)a
(s + t)a = sa + ta
t(a + b) = ta + tb
Beweis:
Das gemischt-assoziative Gesetz s(ta) = (s·t)a
und das erste Distributivgesetz (s + t)a = sa + ta folgen
im Wesentlichen aufgrund der Rechenregeln in
ℝ. Das zweite Distributivgesetz folgt aus dem
ersten Strahlensatz. Dieser Satz besagt, dass für zwei Strahlen, die
den gleichen Anfangspunkt haben und von zwei Parallelen geschnitten
werden, das Verhältnis der Abschnitte auf dem einen Strahl gleich dem
entsprechenden Verhältnis der Abschnitte auf dem anderen Strahl ist.

Die Menge aller Pfeilklassen im Anschauungsraum soll mit ℙ bezeichnet werden. Dann lässt sich die Struktur von ℙ im Hinblick auf die Pfeilklassenaddition zusammenfassend wie folgt beschreiben:
(i)+ a + (b +
c) = (a + b) + c
für alle a, b, c ∈∈ ℙ.
(ii)+ Es existiert o ∈∈
ℙ mit o + a = a
für alle a ∈∈ ℙ.
(iii)+ Zu jedem a ∈∈
ℙ gibt es ein a* ∈∈ ℙ mit a* + a = o.
(iv)+ a + b = b
+ a für alle a, b ∈∈ ℙ.
ℙ ist bezüglich der auf ℙ definierten Addition „+“ aufgrund der Eigenschaften (i)+, (ii)+ und (iii)+ eine Gruppe. Wegen der Gültigkeit des Kommutativgesetzes (Regel (iv)+) ist ℙ sogar eine Abel’sche Gruppe. Das zu jedem a ∈∈ ℙ existierende a* mit a* + a = o ist eindeutig bestimmt und heißt das „zu a inverse Element“. Das Inverse zu a wird üblicherweise mit (−a) bezeichnet.
Im Hinblick auf die Addition gelten in ℙ dieselben Rechengesetze wie in
ℤ,
ℚ
oder
ℝ. Das
bedeutet insbesondere, dass alle weiteren Gesetze, die die
Addition betreffen und im Bereich der Zahlen bereits bewiesen worden sind,
automatisch auch in
ℙ Gültigkeit haben. Umgekehrt gilt natürlich das
Gleiche.
Hierzu gehören beispielsweise die Rechenregeln −(−a) = a
oder −(a + b) = −a − b
oder so etwas wie a + b = a + c ⇒ b = c
und so weiter.
Besondere Eigenschaften eines Dreiecks
![]()
In einem beliebigen Dreieck ABC schneiden sich die drei Seitenhalbierenden in einem Punkt (S), die drei Höhen schneiden sich ebenfalls in einem Punkt (H), das Gleiche gilt für die Mittelsenkrechten mit dem Schnittpunkt M und die Winkelhalbierenden mit dem Schnittpunkt W. Die Punkte M, S und H liegen immer auf einer Geraden, die Eulergerade genannt wird.
Alle oben genannten Aussagen (und viele andere) lassen sich elementargeometrisch (X37, X46, X60, X61, X62) oder aber mit Hilfe von Pfeilklassen beweisen. Als Beispiel soll der folgende Satz dienen:
Die drei Seitenhalbierenden eines Dreiecks schneiden sich in einem
Punkt S.
S teilt jede der Seitenhalbierenden im Verhältnis 1:2.
Beweis:
Gegeben sei ein beliebiges Dreieck ABC.
Dann hat man mit c = AB→
und b = AC→
zwei nicht kollineare Pfeilklassen, das heißt, dass aus der
Gleichung rb + sc = o mit
r, s ∈∈ ℝ
folgt, dass beide Zahlen r und s gleich 0 sein müssen.
 Die Zeichnung liefert die Pfeilklassengleichung
c − b = mv − nw mit zunächst unbekannten Zahlen m und n.
Diese Zahlen m und n existieren, denn irgendwo schneiden sich die
betrachteten Seitenhalbierenden sicherlich.
Die Zeichnung liefert die Pfeilklassengleichung
c − b = mv − nw mit zunächst unbekannten Zahlen m und n.
Diese Zahlen m und n existieren, denn irgendwo schneiden sich die
betrachteten Seitenhalbierenden sicherlich.
Zusammen mit
v = −b + ½c
und w = −c + ½b
ergibt sich durch Einsetzen
c − b = m(−b + ½c) − n(−c + ½b) und hieraus
folgt (−m − ½n + 1)b + (½m + n − 1)c = o.
Da b und c nicht kollinear sind (anschaulich gesprochen: b,
c und c* haben unterschiedliche Richtungen), gilt
−m − ½n + 1 = 0 und ½m + n − 1 = 0.
Dieses Gleichungssystem wird gelöst durch n = 23 und m = 23.
Dieses Resultat ist unabhängig davon, welche zwei Seitenhalbierenden von den drei vorhandenen für die Rechnung ausgewählt werden. Hieraus folgt die Behauptung.
Die strukturellen Eigenschaften der Menge aller Pfeilklassen im Anschauungsraum geben Anlass zu folgender Verallgemeinerung:
Sei (K,+,·) ein Körper mit 0 als Nullelement und 1 als
Einselement, das heißt:
(G) (K,+) und (K\{0},·) sind
Abel’sche Gruppen.
(D) r·(s + t) = r·s + r·t für alle r, s, t ∈∈ K.
Sei ferner (V,+) eine
Abel’sche Gruppe und „·“: KxV
→
V eine Abbildung mit folgenden Eigenschaften:
(GD) s·(t·a)
= (s·t)·a
(D1) (s + t)·a = s·a
+ t·a
(D2) t·(a + b)
= t·a + t·b
(U) 1·a = a
für alle s, t
∈ K und alle a, b
∈ V.
Dann heißt (V,K,·) ein K-Vektorraum, die Elemente von V heißen Vektoren, die Elemente von K nennt man Skalare.
Die Bezeichnungen „Vektor“ und „Skalar“ stammen vom irischen Mathematiker Sir William Rowan Hamilton (1805−1865). Bemerkenswert ist das Axiom (U) (unitäres Gesetz). Stellt man sich unter a eine Pfeilklasse vor, scheint dieses Gesetz selbstverständlich zu sein. Tatsächlich folgt aber (U) nicht aus den anderen Axiomen und muss deshalb als gültig vorausgesetzt werden. Die Aussage des unitären Gesetzes sieht der Rechenregel 1·n = n für n ∈∈ ℕ sehr ähnlich. Auch diese Regel ist − aus mathematischer Sicht − nicht selbstverständlich, kann aber bewiesen werden (→ Beweis).
Alle axiomatisch festgelegten Eigenschaften eines K-Vektorraumes im Einzelnen:
(K) K ist eine nicht leere Menge.
(K+) „+“ ist eine additive Verknüpfung auf K.
(K·) „·“ ist eine multiplikative Verknüpfung auf K.
(i)+ r + (s + t) = (r + s) + t für
alle r, s, t ∈∈ K.
(ii)+ Es existiert 0 ∈ K
mit 0 + r = r für alle r ∈∈ K.
(iii)+ Zu jedem r ∈∈ K
gibt es ein r* ∈ K mit r* + r = 0.
(iv)+ r + s = s + r für
alle r, s ∈∈ K.
(i)* r·(s·t) =
(r·s)·t für alle r, s, t ∈ K.
(ii)* Es existiert 1
∈ K mit 1·r =
r für alle r ∈ K.
(iii)* Zu jedem r ∈ K \ {0} gibt es
ein r* ∈ K \ {0} mit r*·r = 1.
(iv)* r·s = s·r für alle r, s ∈ K.
(D) r·(s + t) = (r·s) + (r·t) für alle r, s, t ∈ K.
(V) V ist eine nicht leere Menge.
(V+) „+“ ist eine additive Verknüpfung auf V.
(I) a +
(b + c) = (a +
b) + c für alle a, b, c ∈ V.
(II) Es existiert o
∈ V mit o + a = a für alle a ∈ V.
(III) Zu jedem a ∈
V gibt es ein a* ∈ V mit a* + a = o.
(IV) a + b = b
+ a für alle a, b ∈ V.
(A) Jedem (r, a)
∈ KxV ist in eindeutiger Weise ein r·a zugeordnet.
(GD) s·(t·a)
= (s·t)·a für
alle s, t ∈ K und alle a ∈ V.
(D1) (s + t)·a = s·a
+ t·a für
alle s, t ∈ K und alle a ∈ V.
(D2) t·(a + b) = t·a + t·b
für alle t ∈ K und alle a, b ∈∈ V.
(U) 1·a = a
für alle a ∈ V.
Das Nullelement 0 ∈ K, das Einselement 1 ∈∈ K sowie das Nullelement o ∈∈ V sind eindeutig bestimmt.
Es folgen vier Beispiele von K-Vektorräumen.
![]() Beispiel 1:
Beispiel 1:
Jeder Körper K ist infolge der Körperaxiome ein Vektorraum
über sich selbst.
Beispielsweise ist
ℝ ein ℝ-Vektorraum.
In diesen speziellen Fällen bedeuten die Operatoren „+“ und „+“ bzw.
„·“ und „·“ dasselbe.
![]() Beispiel 2:
Beispiel 2:
ℙ, die Menge aller Pfeilklassen im Anschauungsraum ist ein ℝ-Vektorraum.
Man beachte, dass in diesem Raum vor allem die Begriffe Punkt,
Richtung und Länge nicht weiter hinterfragt und explizit
definiert, sondern eben anschaulich als gegeben vorausgesetzt werden!
![]() Beispiel 3:
Beispiel 3:
ℝn, induktiv definiert durch
ℝ1 =def
ℝ
ℝm+1 =def
ℝm x
ℝ für alle m = 1, 2, 3...
ist ein ℝ-Vektorraum mit folgenden Definitionen:
(x1, ..., xn) + (y1, ..., yn) =def (x1+y1, ..., xn+yn)
t·(x1, ..., xn) =def
(t·x1, ..., t·xn)
für alle (x1, ..., xn), (y1, ..., yn) ∈ ℝn und alle t ∈ ℝ.
![]() Beispiel 4:
Beispiel 4:
ℱ, die Menge aller reellen Funktionen
(also aller Abbildungen von ℝ
in sich), bildet ein ℝ-Vektorraum mit folgenden Definitionen:
(f + g)(x) =def f(x) + g(x) für alle
x ∈∈ ℝ
(t·f)(x) =def
t·f(x) für alle x ∈∈ ℝ
und t ∈∈ ℝ.
Die Funktion o, definiert durch o(x) = 0 für alle x ∈∈ ℝ ist das Nullelement von ℱ.
Die folgenden zwei Aussagen gelten für alle K-Vektorräume V:
(i) t·a = o
gilt genau dann, wenn t = 0 oder a = o ist.
(ii) (−t)·a = −(t·a)
für alle a ∈∈ V und t ∈∈ K.
Beweis:
(i)
„⇐“:
Mit t = 0 folgt für ein beliebiges a ∈∈ V: 0·a = (0 + 0)·a = 0·a + 0·a.
Wegen (II) und der Tatsache, dass o eindeutig
bestimmt ist, folgt 0·a = o.
Mit a = o folgt für ein beliebiges t ∈∈ K: t·a = t·o = t·(o + o) = t·o + t·o
Also folgt aus demselben Grund wie eben t·o = o.
„⇒“:
Sei t·a = o mit a
∈ V und t
∈ K.
Dann ist entweder t = 0 oder t ǂ 0.
Falls t ǂ 0, dann gibt es wegen (iii)* ein t* ∈∈ K mit t*·t = 1 und es folgt
a = 1·a =
(t*·t)·a = t*·(t·a) =
t*·o = o.
(ii)
Sei a ∈∈ V und t ∈∈ K. Dann gilt t·a + (−t)·a = (t − t)·a = 0·a = o.
Da das Inverse zu jedem Vektor aus V eindeutig bestimmt ist,
folgt die Behauptung.
Diejenigen Pfeile, die den Ursprung eines 3-dimensionalen kartesischen Koordinatensystems als Anfangspunkt haben, werden Ortsvektoren genannt. Jedem Punkt P(p1|p2|p3) mit p1, p2, p3 ∈∈ ℝ kann bei gegebenem Koordinatensystem in bijektiver Weise ein solcher Ortsvektor p zugeordnet werden.
Diejenigen Ortsvektoren, die in die Richtung der Koordinatenachsen zeigen und die Länge 1 haben, sollen Basisvektoren heißen und mit e1, e2 und e3 bezeichnet werden. Dann gilt p = p1·e1 + p2·e2 + p3·e3.
p1, p2 und p3 sind die Koordinaten
des Punktes P, bzw. die Komponenten des Ortsvektors p.
Zwei Ortsvektoren p und q sind genau dann
gleich, wenn für ihre Komponenten unter Verwendung derselben Basis {e1, e2, e3}
gilt:
p1 = q1 und p2 = q2 und p3 = q3.
Den Betrag eines Ortsvektors erhält man, indem der Satz des Pythagoras zweimal angewendet wird:
|p| = √p12+p22+p32
Ein räumliches Koordinatensystem hat üblicherweise die Eigenschaft, rechtshändig zu sein, das heißt: die Richtungen der „positiven“ Achsen werden festgelegt durch Daumen (x1), Zeigefinger (x2) und Mittelfinger (x3) der rechten Hand. Man nennt dies ein Rechtssystem.
Durch die Einführung von Koordinaten gelingt es, geometrische Objekte analytisch zu beschreiben. Dies führt dazu, dass geometrische Probleme auch auf rechnerische Art lösbar werden (analytische Geometrie). Grundlegende Objekte in der analytischen Geometrie sind insbesondere Punkte, Geraden und Ebenen:
t, r und s sind hierbei reelle Parameter; p nennt man sowohl bei Geraden als auch bei Ebenen Stützvektor. Die von o verschiedenen Spannvektoren u und v einer Ebene E müssen immer linear unabhängig sein, das heißt, es gibt keine reelle Zahl k mit u = k·v. Der in der Parametergleichung x = p + t·u verwendete Vektor u, der von o verschieden sein muss, heißt Richtungsvektor.
Addition und S-Multiplikation funktionieren - wie oben bereits definiert - komponentenweise:

Die Aufgaben „Schneiden sich zwei gegebene Geraden, und wenn ja, in welchem Punkt?“ oder „Schneiden sich zwei gegebene Ebenen, und wenn ja, wie lautet die Gleichung der Schnittgeraden?“ oder „In welchem Punkt durchstößt eine gegebene Gerade eine bestimmte Ebene?“ und so weiter, führen im Wesentlichen zur Aufstellung eines linearen Gleichungssystems und dessen Lösung.
![]() Beispiel:
Beispiel:
Gegeben sei eine Gerade g durch ihre Parametergleichung

In welchem Punkt D durchstößt diese Gerade die x1-x2-Koordinatenebene?
Diese Aufgabe wird gelöst mit Hilfe des Gleichungssystems
| x1 = | −3 + 2tD |
| x2 = | 5 − tD |
| 0 = | 6 + tD |
Es folgt tD = −6 und damit x1 = −15 und x2 = 11.
Der gesuchte Durchstoßpunkt ist also D(−15|11|0).
Die Definition des Skalarprodukts liefert eine Möglichkeit, zwei Vektoren miteinander zu multiplizieren. Das Ergebnis des Skalarprodukts zweier Vektoren ist kein Vektor, sondern eine Zahl:
Gegeben seien zwei von o verschiedene, aber ansonsten beliebige Vektoren a, b ∈∈ ℙ, die den Winkel α einschließen. Dann heißt
a•b = |a|·|b|·cos(α)
das Skalarprodukt von a und b. Ist a = o oder b = o, dann setzt man a•b = 0.

Für 0°≤ α < 90° und 270° < α ≤ 360° ist a•b positiv; für 90° < α < 270° ist a•b negativ; a•b = 0, wenn α = 90° oder α = 270°.
Hiermit lässt sich der geometrische Sachverhalt, dass zwei geometrische Objekte senkrecht zueinander stehen, auch analytisch ausdrücken:
a ⊥ b ⇔ a•b = 0 mit a, b ǂ o
Außerdem folgt direkt aus der Definition des Skalarprodukts a•a = |a|2 für alle a ∈∈ ℙ, kurz geschrieben:
a2 = a2 für alle a ∈∈ ℙ.
Physikalisch ist das Skalarprodukt überall dort bedeutsam, wo es um die Berechnung von Energiemengen geht und hierbei gerichtete Größen eine Rolle spielen. Zwei Beispiele: Für die Verschiebung eines Körpers um einen gewissen Streckenabschnitt Δs durch eine konstante Kraft F muss insgesamt die Energie ΔW = F•Δs aufgebracht werden. ändert irgendein sich mit der Geschwindigkeit v gleichförmig bewegtes System seinen Impuls um ΔP, dann nimmt es hierbei den Energiebetrag ΔW = v•ΔP auf.
Elementargeometrisch folgen für alle
a, b, c ∈∈ ℙ und alle t ∈∈ ℝ die folgenden Rechenregeln:
(S1) a•b = b•a
(Kommutativgesetz)
(S2) a•(b + c) =
a•b + a•c
(Distributivgesetz)
(S3) a•(t·b) = (t·a)•b = t·(a•b)
(gemischt assoziatives Gesetz)
Diese Regeln folgen mit den in ℝ gültigen Rechenregeln auch aus der Aussage des folgenden Satzes:
Sind a und b durch ihre Koordinaten a1, a2 und a3 bzw. b1, b2 und b3 in einem 3-dimensionalen kartesischen Koordinatensystem gegeben, dann gilt
a • b = a1·b1 + a2·b2 + a3·b3
Beweis:
Jedes beliebige Dreieck ABC lässt sich unter
Benutzung einer der Höhen in zwei rechtwinklige Dreiecke zerlegen.

Sind a und b durch ihre Komponenten gegeben,
so folgt mit dem Kosinussatz
a • b
= a·b·cos(γ)
= 12(a2 + b2 − |a − b|2)
= a1·b1 + a2·b2 + a3·b3.
Mit Hilfe des Skalarproduktes kann man eine Ebene E parameterfrei durch eine Normalengleichung beschreiben: Hat man einen auf der Ebene E senkrecht stehenden Vektor n, so gilt für alle Punkte X auf E:
(x − p)•n = 0.

n heißt Normalenvektor der Ebene E. Benutzt man speziellerweise einen normierten Normalenvektor n0, dann gilt definitionsgemäß |n0| = 1 und
(x − p)•n0 = 0
heißt Hesse’sche Normalenform.
Wendet man den eben bewiesenen Satz auf eine Normalengleichung von E an, so ergibt sich
n1·x1 + n2·x2 + n3·x3 = d
mit d = p1n1 + p2n2 + p3n3. Umgekehrt gilt:
Die Koordinatengleichung a·x1 + b·x2 + c·x3 = d mit a, b, c, d ∈∈ ℝ beschreibt immer eine Ebene und der Vektor mit den Koordinaten a, b und c ist ein Normalenvektor der Ebene.
Beweis:
Gegeben sei die Koordinatengleichung a·x1 + b·x2 + c·x3 = d
mit beliebig gewählten reellen Zahlen a, b, c und d.
Seien e1, e2, e3
die Basisvektoren des Koordinatensystems und
n = a·e1 + b·e2 + c·e3
bzw. x = x1·e1 + x2·e2 + x3·e3,
dann lässt sich die gegebene Gleichung auch so schreiben:
n•x = d.
Zum Vektor
n und zur Zahl d gibt es immer
irgendeinen Vektor p mit
n•p = d.
Hieraus folgt
n•x = n•p
und damit
n•x − n•p = n•(x − p) = 0.
Diese Gleichung aber ist die Normalengleichung einer Ebene,
p ist ein zu einem Punkt der Ebene gehörender Ortsvektor
und
n ist senkrecht zu dieser Ebene.
Ist (x − p)•n0 = 0 die zu einer Ebene E gehörende Hesse'sche Normalenform und R(r1|r2|r3) irgendein Punkt, dann gilt für die Länge des Lotes von R auf E
d = |(r − p)•n0|.
d heißt Abstand des Punktes R von der Ebene E.
Beweis:
Sei F der Fußpunkt des Lotes von R auf E und d der Abstand zwischen R und F.

Dann gilt PR→•n0 = |PR|·1·cos(α) = d sowie PR*→•n0 = |PR*|·cos(α*) = |PR*|·cos(180°−α) = −d.
Mit r − p = PR→ folgt die Behauptung.
Der Begriff des Skalarprodukts lässt sich verallgemeinern.
Sei (K,+,·) irgendein Körper und „*“: K → K
eine bijektive Abbildung mit
(s + t)* = s* + t*; (s·t)* = s*·t* und (t*)* = t für alle s, t ∈∈ K.
Seien ferner (V,K,·) und (W,K,·)
zwei K-Vektorräume.
Dann heißt eine Abbildung f: VxW → K
eine Semibilinearform,
wenn für alle v, v’ ∈∈ V; w, w’ ∈∈ W und
alle t ∈∈ K Folgendes gilt:
(i) f(v+v’, w) = f(v, w) + f(v’, w)
(ii) f(v , w+w’) = f(v, w) + f(v, w’)
(iii) f(t·v, w) = t·f(v, w)
(iv) f(v, t·w) = t*·f(v, w)
Gilt für alle t ∈∈ K t = t*, so
heißt f
Bilinearform.
Im Fall V = W schreibt man dann statt f(v, w)
üblicherweise ⟨v,
w⟩.
![]() Beispiel 1:
Beispiel 1:
„*“: ℂ → ℂ
sei diejenige Abbildung, die jeder komplexen Zahl x+iy die konjugiert
komplexe Zahl x−iy zuordnet.
Dann ist die Abbildung f:
ℂnxℂn → ℂ
mit
f(v, w) =def (v1·w1* + ... + vn·wn*)
eine Semibilinearform. Hierbei ist v = (v1, v2, ... vn) ∈∈ ℂn und w = (w1, w2, ... wn) ∈∈ ℂn.
![]() Beispiel 2 (Standard-Skalarprodukt):
Beispiel 2 (Standard-Skalarprodukt):
„⟨,⟩“:
ℝnxℝn → ℝ mit
⟨v, w⟩ =def (v1·w1 + ... + vn·wn)
ist eine Bilinearform. Hierbei ist v = (v1, v2, ... vn) ∈∈ ℝn und w = (w1, w2, ... wn) ∈∈ ℝn.
Eine Semibilinearform f: V2 → K heißt genau dann eine symmetrische Form, wenn
f(v, w) = f(w, v) für alle v,w ∈∈ V.
Eine Semibilinearform f: V2 → K heißt genau dann eine Hermite’sche Form, wenn
f(v, w) = (f(w, v))* für alle v, w ∈∈ V.
Ist V ein K-Vektorraum und f: V2 → K eine symmetrische oder eine Hermite'sche Form, dann heißt (V,f) ein metrischer Vektorraum.
Ist K = ℝ oder K = ℂ, dann heißt eine symmetrische oder eine Hermite’sche Form f genau dann positiv definit, wenn
f(v, v) > 0 für alle v ∈∈ V mit v ǂ o und f(o, o) = 0.
Sei V ein ℝ-Vektorraum und „⟨,⟩“: V2 → ℝ eine symmetrische und positiv definite Bilinearform, dann heißt diese Bilinearform Skalarprodukt von V.
Ein ℝ-Vektorraum mit einem Skalarprodukt heißt euklidischer Vektorraum.
Mit Hilfe des Skalarproduktes ist es möglich, Längen zu messen. Hierzu wird der Betrag eines Vektors v als Element eines euklidischen Vektorraums wie folgt definiert:
|v| = √⟨v, v⟩ für alle v ∈∈ V
In einem euklidischen Vektorraum (V,⟨,⟩) gilt die Cauchy-Schwarz’sche Ungleichung
|⟨v, w⟩| ≤ |v|·|w| für alle v, w ∈∈ V.
Beweis:
Sei o das Nullelement von V.
Fall 1: v =
w = o.
Es gilt |⟨o, o⟩| = 0 und |o|·|o| = 0·0 = 0.
Fall 2: Entweder v = o oder
w = o.
Wegen der Symmetrie von ⟨,⟩ reicht es, eine dieser zwei
Möglichkeiten zu behandeln.
Sei also beispielsweise v = o und
w ∈∈ V
beliebig gewählt. Dann gilt
⟨o, w⟩ = ⟨o+o, w⟩
= ⟨o,
w⟩ + ⟨o, w⟩.
⟨o, w⟩ muss also das Nullelement in
ℝ
sein, mit anderen Worten:
⟨o, w⟩ = 0. Außerdem gilt |o|·|w| = 0·|w| = 0.
Fall 3: v
ǂ o und w
ǂ o. Dann gilt für alle t ∈∈ ℝ:
0
≤ ⟨v − t·w,
v − t·w⟩
= ⟨v, v⟩ − 2·t·⟨v, w⟩ + t2·⟨w,
w⟩.
⟨w, w⟩ ist wegen
w
ǂ o verschieden von 0.
Setzt man t = ⟨v,
w⟩/⟨w, w⟩, so folgt aus
0 ≤ ⟨v,
v⟩ − 2·t·⟨v,
w⟩ + t2·⟨w,
w⟩ die Ungleichung
0 ≤ ⟨v,
v⟩·⟨w,
w⟩ − ⟨v,
w⟩·⟨v,
w⟩. Dies ist
gleichbedeutend mit
⟨v, w⟩2 ≤ ⟨v,
v⟩·⟨w,
w⟩ = |v|2·|w|2
und hieraus folgt
wegen |v| > 0 und |w| > 0 die Behauptung.
Aus der Cauchy-Schwarz’schen Ungleichung folgt zum Beispiel unmittelbar für alle vi, wi ∈∈ ℝ und n ∈∈ ℕ*:
(v1·w1 + ... + vn·wn)2 ≤ (v12 + ... + vn2)·(w12 + ... + wn2).
In einem euklidischen Vektorraum (V,⟨,⟩) gilt die Dreiecksungleichung
|v + w| ≤ |v|+|w| für alle v, w ∈∈ V.
Beweis:
Seien v, w ∈ V beliebig
gewählt. Dann gilt
|v +
w|2
= ⟨v +
w, v
+ w⟩
= ⟨v +
w, v⟩
+
⟨v
+ w, w⟩
= ⟨v,
v⟩ + ⟨w, v⟩
+ ⟨v ,
w⟩ + ⟨w, w⟩
≤ |v|2 + 2·|v|·|w|
+ |w|2
= (|v| + |w|)2
Hieraus folgt die Behauptung.
Sei (V,⟨,⟩) ein euklidischer Vektorraum mit o als Nullelement.
Dann heißt eine Abbildung „∥ ∥“: V → ℝ
mit folgenden Eigenschaften
∥t·v∥ = |t|·∥v∥
für alle v ∈∈ V
und alle t ∈∈ ℝ
∥v
+ w∥
≤ ∥v∥
+ ∥w∥
für alle v, w ∈∈ V
∥v∥ = 0
⇔ v
= o für alle
v ∈∈ V
eine Norm von V.
|v| = √⟨v, v⟩ für alle v ∈∈ V
hat diese drei Eigenschaften und heißt euklidische Norm von V.
Bewegt sich eine elektrische Ladung q mit der Geschwindigkeit v senkrecht zu einem homogenen Magnetfeld, dann wirkt auf sie die Lorentzkraft F. Diese Kraft F steht sowohl senkrecht auf v, als auch auf dem Vektor B, mit dem die Stärke des Magnetfeldes gemessen wird. Für den Betrag der Lorentzkraft gilt F = |F| = |q|·v·B.

Die Richtung von F wird mit der Dreifingerregel ermittelt: Der Daumen gibt die Bewegungsrichtung der Ladung an, der Zeigefinger weist in die Richtung der Magnetfeldlinien, der Mittelfinger zeigt die Richtung der Lorentzkraft an. Bei negativen Ladungen nimmt man die linke Hand (wie zum Beispiel in der Abbildung), für positive Ladungen ist die rechte Hand zuständig. Die Wirkung der Lorentzkraft erkennt man beim Überfahren der Abbildung mit dem Mauszeiger.
Bewegt sich q schräg zu den B-Feldlinien, dann ist für die Berechnung von F nur diejenige Komponente von v bedeutsam, welche senkrecht zu B steht, das bedeutet: F = |q|·v·B·|sin(α)|, wobei α den Winkel bezeichnet, der von v und B eingeschlossen wird. Kurz geschrieben: F = |q·vxB|. Die hier verwendete Verknüpfung „x“ wird wie folgt erklärt:
Gegeben seien zwei von o verschiedene, aber ansonsten beliebige Vektoren a, b ∈∈ ℙ, die den Winkel α einschließen.
![Rechtssystem [a, b, axb]](images/axb.gif)
Dann sei axb ∈∈ ℙ definiert durch folgende Eigenschaften:
(i) axb ⊥ a und axb ⊥ b
(ii) [a, b, axb]
ist ein Rechtssystem (siehe Abb.)
(iii) |axb| = |a|·|b|·|sin(α)|
axb heißt Kreuzprodukt (oder Vektorprodukt) von a und b.
Ist a = o oder b = o, dann setzt man axb = o.
Nach dieser Definition ist axb ein Normalenvektor der durch a und b festgelegten Ebene und der Betrag von axb entspricht dem Flächeninhalt des von a und b aufgespannten Parallelogramms. So wie Orthogonalität mit Hilfe des Skalarproduktes analytisch beschreibbar ist, lässt sich mit Hilfe des Kreuzproduktes Parallelität analytisch beschreiben, denn es gilt nach Definition wegen (iii)
a || b ⇔ axb = o mit a, b ǂ o
Ferner gelten für alle a, b, c ∈∈ ℙ und alle t ∈∈ ℝ die folgenden Rechenregeln:
(K1) axb = − bxa
(K2) ax(b + c) = axb
+ axc
(Distributivgesetz)
(K3) ax(t·b)
= t·(axb)
(gemischt assoziatives Gesetz)
Beweis:
(K1) und (K3) folgen direkt aus der Definition.
(K1) bedeutet, dass das Kommutativgesetz bezüglich „x“ nicht
gilt!
zu (K2):
Falls a = o oder b = o
oder c = o, ist nichts zu beweisen.
Seien also im Folgenden a, b und c verschieden von o.
a = PA→, b = PB→, c = PC→.
E sei diejenige Ebene durch den Punkt P, die a als Normalenvektor hat.
Seien bE und cE die
Vektoren, die aus b bzw. c durch Projektion auf E entstehen.

Dann gilt axb = axbE. (Das aus a und b gebildete Parallelogramm und das aus a und bE gebildete Parallelogramm sind flächengleich!) Entsprechend gilt axc = axcE sowie ax(b+c) = ax(bE+cE).
Also ist (K2) äquivalent mit ax(bE + cE) = axbE + axcE.
Wegen a ⊥ bE und a ⊥ cE gilt |axbE| = a·bE und |axcE| = a·cE.
a·bE und a·cE sind die Längen des von axbE und axcE aufgespannten und in E liegenden Parallelogramms Pa. bE und cE sind die Längen des von bE und cE aufgespannten Parallelogramms P1. Diese beiden Parallelogramme sind ähnlich und die entsprechenden Seiten stehen senkrecht aufeinander.

Auch die Diagonalen beider Parallelogramme stehen aufeinander senkrecht.
Bezeichnet man mit da bzw. d1 die Längen der
Diagonalen der entsprechenden Parallelogramme, dann gilt
da = a·d1, mit anderen Worten: |axbE + axcE| = a·|bE + cE|.
a, bE+cE, axbE+axcE
stehen paarweise aufeinander senkrecht und bilden in dieser Reihenfolge
ein Rechtssystem.
Hieraus folgt ax(bE + cE) = axbE + axcE und damit (K2).
Sind a und b durch ihre Koordinaten a1, a2 und a3 bzw. b1, b2 und b3 in einem 3-dimensionalen kartesischen Koordinatensystem gegeben, dann gilt
a x b = (a2b3−a3b2)·e1 + (a3b1−a1b3)·e2 + (a1b2−a2b1)·e3
(Hierbei sind e1, e2, e3 die Basisvektoren des Koordinatensystems.)
Beweis:
Sei a = a1·e1
+ a2·e2
+ a3·e3
und b = b1·e1
+ b2·e2
+ b3·e3.
Es gilt e1xe2 = e3, e2xe3 = e1 und e3xe1 = e2.
Ferner gilt e1xe1 = e2xe2 = e3xe3 = o.
Dann folgt unter Beachtung des Distributivgesetzes (K2):
a x b
= (a1·e1+a2·e2+a3·e3) x
(b1·e1+b2·e2+b3·e3)
= a1b2·e3
− a1b3·e2
− a2b1·e3
+ a2b3·e1
+ a3b1·e2
− a3b2·e1
= (a2b3−a3b2)·e1
+ (a3b1−a1b3)·e2
+ (a1b2−a2b1)·e3
Skalare Felder und Vektorfelder
![]()
In diesem Abschnitt werden Vektoren mit fetten Buchstaben ohne Unterstrich bezeichnet.
Gehört zu jedem Ort x= (x1,x2,x3) eines
zusammenhängenden und offenen Raumgebietes G ⊆ ℝ3 ein Wert
einer skalaren Funktion f(x) oder ein Wert einer vektoriellen Funktion v(x) = (v1(x),v2(x),v3(x)), so wird hiermit ein skalares Feld bzw. ein
Vektorfeld definiert. Die Punktkoordinaten x1, x2
und x3 beziehen sich hierbei auf ein bestimmtes dreidimensionales kartesisches Koordinatensystem.
Die Temperaturverteilung in der Erdatmosphäre oder die Dichteverteilung in einem Festkörper sind zum Beispiel skalare Felder; Beispiele für Vektorfelder sind E- und B-Felder (elektrische und magnetische Felder), das Gravitationsfeld der Erde oder das Geschwindigkeitsfeld in einer strömenden Flüssigkeit. Ein skalares oder ein vektorielles Feld, das sich mit der Zeit nicht ändert, heißt stationär.
Skalare Felder lassen sich mit Hilfe von Niveauflächen veranschaulichen: für alle Punkte einer Niveaufläche hat die Funktion f einen konstanten Wert.
Ein Vektorfeld kann man mit Hilfe von Feldlinien darstellen: jeder vektorielle Wert der Funktion v ist an jedem Punkt in G tangential zur jeweiligen Feldlinie orientiert. Hat speziellerweise v überall in G denselben Wert, nennt man das zugehörige Feld homogen. Die Feldlinien sind dann zueinander parallele Geraden.
Macht man in einem skalaren Feld von einem Ort x aus einen kleinen Schritt zu irgendeinem dicht benachbarten Ort x+dx mit dx = (dx1,dx2,dx3), so ändert sich der Wert der Funktion f dort um
df = ∂f∂x1dx1 + ∂f∂x2dx2 + ∂f∂x3dx3
wobei f hier als stetig differenzierbar vorausgesetzt wurde.
Die rechte Seite dieser Gleichung kann man als Skalarprodukt zweier Vektoren auffassen:
df = grad f • dx
Hierbei wird definiert:
Sei G
⊆ ℝ3 ein Gebiet und f eine auf G definierte und stetig
differenzierbare Funktion. Dann heißt
grad f = (∂f∂x1, ∂f∂x2, ∂f∂x3)
der Gradient von f.
grad f ist ein wohldefinierter Vektor, denn unabhängig vom verwendeten Koordinatensystem ergibt sich durch die Formel df = grad f • dx immer dasselbe Resultat für df.
Beweis:
Sei mit edx der Einheitsvektor in der durch
dx = (dx1,dx2,dx3)
gegebenen Richtung bezeichnet.
Schreibt man für den Betrag von dx statt |dx|
kurz dx, dann gilt dx = dx·edx
und dxi = dx·cos(edx,xi)
für i = 1, 2, 3.
cos(edx,xi) ist der Kosinus des von edx
und der xi-Achse eingeschlossenen Winkels.
Aus
df = ∂f∂x1dx1 + ∂f∂x2dx2 + ∂f∂x3dx3
folgt dann
dfdx = ∂f∂x1cos(edx,x1) + ∂f∂x2cos(edx,x2) + ∂f∂x3cos(edx,x3).
Kurz geschrieben:
dfdx = grad f • edx.
Das Skalar dfdx ist die Änderung von f pro Längeneinheit in einer durch edx beliebig vorgegebenen Richtung, und zwar unabhängig von der Wahl des Koordinatensystems hingeschrieben. Hieraus folgt die Behauptung.
Bewegt man sich ein wenig entlang einer Niveaufläche, dann ist dx tangential zu dieser Fläche orientiert und es gilt df = 0. Also steht der Gradient von f senkrecht zur Niveaufläche und weist damit stets in die Richtung des größten Anstiegs von f. Der Betrag von grad f ist gerade diese Änderung von f pro Längeneinheit.
Für grad f gibt es eine abkürzende Schreibweise:
grad f = ∇f
Der hier verwendete Nabla-Operator
∇ = (∂∂x1, ∂∂x2, ∂∂x3)
ist ein symbolischer oder formaler Vektor, genauer gesagt: ein vektorieller Differentialoperator mit Invariantencharakter. Man kann (und muss) nachrechnen, dass sich die Komponenten von ∇ bei zulässigen Transformationen des verwendeten kartesischen Koordinatensystems sich genauso verhalten wie die Koordinaten x1, x2 und x3.
∇f ist so etwas wie die
multiplikative Verknüpfung von ∇
mit der skalaren Größe f.
Entsprechend gibt es die Möglichkeit, das Skalarprodukt bzw. das
Vektorprodukt mit ∇ und einer
Vektorfunktion v zu definieren:
Sei G ⊆ ℝ3 ein Gebiet und v mit v(x) = (v1(x),v2(x),v3(x)) eine
auf G definierte Vektorfunktion.
v1,v2 und v3 seien überall auf G stetig
differenzierbar.
Dann heißt div v = ∇•v
Divergenz von v und rot v = ∇xv
Rotation von v.
Es gilt demnach
div v = ∂∂x1v1 + ∂∂x2v2 + ∂∂x3v3
und
rot v = (∂v3∂x2 − ∂v2∂x3)e1 + (∂v1∂x3 − ∂v3∂x1)e2 + (∂v2∂x1 − ∂v1∂x2)e3
Hierbei sind e1, e2, e3 die Basisvektoren des verwendeten kartesischen Koordinatensystems.
Mit Hilfe der vorstehend definierten Begriffe und Schreibweisen lassen sich insbesondere die Maxwell-Gleichungen auf sehr elegante Weise formulieren. Die von James Clerk Maxwell (1831−1879) aufgestellten Gleichungen beschreiben, wie elektrische und magnetische Felder miteinander zusammenhängen. Eine seiner insgesamt vier Gleichungen ist das Induktionsgesetz
rot E = − ∂B∂t.
Diese Gleichung beschreibt, dass und auf welche Weise ein E-Feld entsteht, wenn sich ein B-Feld zeitlich ändert. Hierbei ist E die elektrische Feldstärke und B die magnetische Feldstärke (historisch: magnetische Flussdichte).
Eine weitere Gleichung lautet:
div B = 0.
Dies bedeutet, dass ein B-Feld stets quellenfrei ist, mit anderen Worten: es gibt keine magnetischen Monopole.
